Объединение всех подмножеств совпадает с множеством Х

Разбиение множества на классы называют классификацией.

V. Декартово произведение множеств

Декартовым произведением множеств А и В называется множество пар, первая компонента каждой из которых принадлежит множеству А, а вторая — множеству В Декартово произведение множеств А и В обозначают А х В. Таким образом, А×В={(x,y)|x∈A˄y∈B}. Операцию нахождения декартова произведения множеств А и В называют декартовым умножением этих множеств. Если А и В — числовые множества, то элементами декартова произведения этих множеств будут упорядоченные пары чисел.

VI. Правила суммы и произведения

Обозначим число элементов конечного множества A символом n(A). Если множества А и В не пересекаются, то n(AUВ)= n(А) +n (В). Если множества А и В пересекаются, то n(А U В) = n (A) + n (В) — n (A ∩ В).

Число элементов декартова произведения множеств A и В подсчитывается по формуле n (А X В) = n (A) • n (В).

Правило подсчета числа элементов объединения непересекающихся конечных множеств в комбинаторике носит название правила суммы, если элемент х можно выбрать k способами, а элемент у — m способами, причем ни один из способов выбора элемента х не совпадает со способом выбора элемента у, то выбор «х или у» можно осуществить k + m способами.

Правило подсчета числа элементов декартова произведения конечных множеств в комбинаторике носит название правила произведения: если элемент х можно выбрать k способами, а элемент y - m способами, то пару (х,y) можно выбрать km способами.

Мощность множества

Мощность множества, или кардинальное число множества, - характеристика множеств (в том числе бесконечных), обобщающее понятие количества (числа) элементов конечного множества.

В основе этого понятия лежат естественные представления о сравнении множеств:

Любые два множества, между элементами которых может быть установлено взаимно однозначное соответствие ( Биекции), содержат одинаковое количество элементов (имеют одинаковую мощность).
Обратно: множества, равные по мощности, должны допускать такое взаимно однозначное соответствие.
Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).

К построению теории мощности множеств, множества различались по признакам: пустая / непустое и конечное / бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.

Мощность множеств позволяет сравнивать бесконечные множества. Например счетное множества являются самыми "маленькими" бесконечными множествами.

Мощность множества 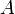обозначается через 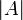. Сам Кантор использовал обозначения 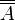. Иногда встречаются обозначения 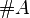и .

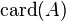Мощность конечных множеств

Для множеств с конечным числом элементов, мощность множества является фактически количеством элементов этого множества. Иначе можно сказать, что множество A является конечным, если существует такое натуральное число n, что A ~ {k, k ∈ N ∧ k ≤ n}. В противном случае, множество называется бесконечным.

Между двумя конечными множествами A и B существует взаимно однозначное соответствие тогда и только тогда, когда их мощности совпадают, т.е. | A | = | B |.

Пусть A = {a _1, a _2,..., a _n} - конечное множество с n элементов (| A | = n), тогда количество всех подмножеств множества A равна 2 ^n, т.е. 2 ^{| A |.}

Множество всех подмножеств некоторого множества A (конечной или бесконечной) часто обозначают через β (A) (или B (A) или 2 ^{| A |)} и называют Булеан множества A. Очевидно, что для конечного множества A выполняется | B (A) | = 2 ^{| A |.}

Дата добавления: 2018-04-04; просмотров: 369; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 Следующая ⇒

Мы поможем в написании ваших работ!