Алгоритм применения t-критерия Стьюдента для сравнения оценки средних величин двух выборок
1. Записать вариационный ряд результатов x экспериментальной группы и y контрольной группы.
2. Найти выборочные средние и выборочные дисперсии
3. Вычислить эмпирическое значение критической статистики и сравнить его с критическим значением tкрит

n и m – число ячеек для переменных x и y соответственно
Критическое значение tкрит определяется по таблице для уровня значимости α и степеней свободы r=n+m-2 .
Если tэьпир>tкрит, то различия между средними значениями экспериментальной и контрольной групп существенны на данном уровне значимости.
Сравнение двух средних нормальных генеральных совокупностей.
Пример: для представленных данных, используя t-критерий Стьюдента на 1%-м уровне значимости, докажите достоверность различия между средними величинами опыта и контроля.
| эксперимент | 5 | 6 | 7 | 6 | 7 | 
|
| контроль | 1 | 2 | 2 | 2 | 1 | 
|
 7
7

 =
= 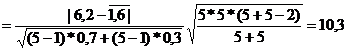
tэьпир>tкрит=3,36 поэтому нулевую гипотезу о незначительности различия между средними величинами опыта и контроля отвергают.
Проверка гипотезы о значимости выборочного коэффициента корреляции (нулевая гипотеза - равенство нулю коэффициента корреляции)
Пример: определите, существует ли корреляционная связь между рождаемостью и смертностью для городов Ярославской области.
| Города | Ярославль | Рыбинск | Переславль | Ростов | Тутаев | Углич |
| Рождаемость | 104,9 | 102,7 | 114,8 | 124,1 | 104,0 | 119,3 |
| Смертность | 103,4 | 99,5 | 103,0 | 102,5 | 114,0 | 105,9 |
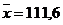

|
|
|
 ,
, 
Вычислим выборочную ковариацию
k(x,y)=1/6[(104,9-11,6)*(103,4-104,7) + (119,3-11,6)*(105,9-104,7)]= -0,7
Вычислим выборочный коэффициент корреляции

Вычислим наблюдаемое значение критерия

Для уровня значимости в 0,1 и степеней свободы r=n-2=4
 – нет оснований отвергать нулевую гипотезу (r =0).
– нет оснований отвергать нулевую гипотезу (r =0).
Вопросы для самоконтроля
1. Назовите основные типы статистических критериев проверки гипотезы.
2. В каких случаях применяются критерии Стьюдента и Пирсона?
3. Как определяются степени свободы?
4. Какие выборки следует считать однородными?
5. Какие критерии однородности вы знаете? Каковы условия применимости этих критериев?
6. Почему в критерии хи- Пирсона не может быть недопустимо малых значений критической статистики?
7. Коэффициенты ранговой корреляции Спирмена, Кендалла и критические точки распределения Стьюдента.
8. Приведите примеры практических задач, когда необходима проверка гипотез о равенстве математических ожиданий, дисперсий.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задача 1. По выборке объема n=16, извлеченной из нормальной генеральной совокупности, найдены выборочное среднее (59,1) и среднее квадратическое отклонение (1,8). Проверьте нулевую гипотезу (равенство средних в значении 60) при уровне значимости 0,05.
|
|
|
Задача 2. Проектный контролируемый размер изделий, изготавливаемых станком-автоматом, составляет 25мм. Проверьте нулевую гипотезу равентсва средних генеральной совокупности и выборки на уровне значимости 0,05.
Измерения 20 случайно отобранных изделий дали результаты:
| Контролируемый размер | 24,8 | 24,9 | 25,0 | 25,1 | 25,3 |
| Число изделий | 2 | 3 | 4 | 6 | 5 |
Задача 3. Физическая подготовка 10 спортсменов была проверена при поступлении на факультет физической культуры, а затем после первого семестра. Установите при уровне значимости 0,1, значимо или незначимо улучшилась физическая подготовка спортсменов, в предположении, что число баллов распределено нормально. Итоги проверки в баллах:
| Число баллов при поступлении | 75 | 72 | 55 | 48 | 60 | 68 | 28 | 65 | 58 | 71 |
| Число баллов после 1 семестра | 80 | 85 | 51 | 52 | 60 | 62 | 35 | 83 | 61 | 87 |
Задача 4. Известны следующие выборочные данные о посеве яровых за день (в процентах к плану) хозяйствами области: 3, 4, 7, 1, 3, 3, 1, 5, 6, 2, 4, 3, 4, 5, 2, 2, 4, 3, 5, 6, 4, 3, 2, 5, 4.
Составьте вариационный ряд, постройте полигон относительных частот и проверьте по критерию Пирсона, нормальность распределения.
|
|
|
Задача 5. Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать 0,1. Проверьте, обеспечивает ли станок требуемую точность при уровне значимости 0,05. Взята проба из 25 случайно отобранных изделий, которая дала результаты измерений:
| контролируемый размер | 3,0 | 3,5 | 3,8 | 4,4 | 4,5 |
| частота | 2 | 6 | 9 | 7 | 1 |
Задача 6. Исследование в течение 10 дней производительности двух предприятий, выпускающих стиральные машины, дало следующие результаты:
| 1-е предприятие | 82 | 74 | 64 | 72 | 84 | 68 | 76 | 88 | 75 | 60 |
| 2-е предприятие | 52 | 63 | 72 | 64 | 48 | 70 | 78 | 68 | 75 | 54 |
Можно ли считать одинаковыми распределения производительности выпуска стиральных машин на обоих предприятиях при уровне значимости в 0,05?
Задача 7. Во время медосбора были получены следующие выборочные данные о суточной прибавке меда на пасеках области:
| Суточная прибавка (кг.) | 3 - 4 | 4 - 5 | 5 - 6 | 6 - 7 | 7 - 8 | 8 - 9 |
| Количество пчелосемей | 6 | 26 | 55 | 45 | 15 | 3 |
Подчиняется ли суточная прибавка меда нормальному закону?
Задача 8. Найдите коэффициент ранговой корреляции для измерениями двумя приборами шести деталей (в сотых долях миллиметра):
|
|
|
| xi | 11 | 10 | 12 | 9 | 13 | 8 |
| yi | 12 | 9 | 13 | 8 | 14 | 7 |
Установите, при каком уровне значимости ранговая корреляционная связь будет значимой.
Задача 9. Результаты выборочного обследования коров стада одного сельхозпредприятия по годовому надою приведены в таблице:
| Годовой надой (тыс кг.) | 2,7-2,9 | 2,9-3,1 | 3,1-3,3 | 3,3-3,5 | 3,5-3,7 | 3,7-3,9 | 3,9-4,1 | 4,1-4,3 |
| Количество коров | 5 | 16 | 33 | 43 | 37 | 20 | 7 | 2 |
Выясните, является ли распределение годового надоя нормальным. Найдите процент надоев в среднем по хозяйству не менее 3500 кг и процент коров, у которых средний годовой надой отличается от среднего годового надоя по хозяйству меньше чем на 500 кг.
Задача 10. По выборке объема 100, известной из двумерной нормальной генеральной совокупности, составлена корреляционная таблица:
| Y Х | 10 | 15 | 20 | 25 | 30 | 35 | nx |
| 25 | 5 | 1 | - | - | - | - | 6 |
| 35 | - | 6 | 2 | - | - | - | 8 |
| 45 | - | - | 5 | 40 | 5 | - | 50 |
| 55 | - | - | 2 | 8 | 7 | - | 17 |
| 65 | - | - | - | 4 | 7 | 8 | 19 |
| ny | 5 | 7 | 9 | 52 | 19 | 8 | n=100 |
Найдите коэффициент корреляции и проверьте нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при уровне значимости 0,05.
Ранговые корреляции
Необходимость в применении ранговых корреляций возникает в двух случаях: когда распределение хотя бы одной из двух переменных не соответствует нормальному и когда связь между переменными является нелинейной (но монотонной). В этих случаях вместо корреляции r Пирсона можно выбрать ранговые корреляции: r Спирмена или «тау» Кендалла. Программа предварительно ранжирует переменные, связь между которыми вычисляется.
Корреляцию r Спирмена программа SPSS вычисляет следующим образом. Сначала переменные переводятся в ранги, а затем к рангам применяется формула расчета r Пирсона. Таким образом, r Спирмена интерпретируется по аналогии с r Пирсона.
Иначе дело обстоит с корреляцией тау Кендалла, которая имеет вероятностную природу.
Пример: оценка связи между ростом и весом в группе людей, предварительно ранжированных по этим переменным. Тогда при сравнении любых двух человек из этой группы возможны две ситуации:
Ø однонаправленное изменение переменных («совпадение»), когда и большему росту соответствует больший вес;
Ø разнонаправленное изменение («инверсия»), когда чем больше рост тем вес меньше.
Перебрав все пары испытуемых, можно оценить вероятность совпадений (P) и вероятность инверсий (Q).
Корреляция Кендалла – это разность вероятностей «совпадений» и «инверсий»:
τ = P – Q.
Как и большинство статистических процедур, команды подменю Корреляции наряду с описательными статистиками (корреляциями в данном случае) вычисляют их уровень значимости.
Уровень значимости является мерой статистической достоверности результата вычислений, в данном случае — корреляции, и служит основанием для интерпретации.
Если уровень значимости корреляции не превышает 0,05 – корреляция является случайной с вероятностью не более 5 %. Обычно это является основанием для вывода о статистической достоверности корреляции.
В противном случае (p > 0,05) связь признается статистически недостоверной и не подлежит содержательной интерпретации.
SPSS позволяет определять два теста значимости: односторонний и двухсторонний. Обычно используется двухсторонний тест значимости. Но если вы заранее знаете направление корреляции (положительное или отрицательное) и вас интересует только одно направление, можно использовать односторонний тест значимости. Однако такая ситуация встречается редко, а если и встречается, то правомерность односторонней проверки с трудом поддается обоснованию.
Пример: найти коэффициент ранговой корреляции Спирмена по связи эмоционального состояния и зрительной памяти. Использовать Преобразовать/Ранжировать наблюдения (число групп составляет 24). Сравнить со значением к. Кендалла, рассчитанным в программе SPSS
| Количество выборов, соответствующее положительному эмоциональному состоянию | Зрительная память | 
| 
| ||
| баллы | ранг | баллы | ранг | ||
| 3 | 19.5 | 6 | 22 | -2,5 | 6,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 1 | 3,5 | 4 | 7 | -3,5 | 12,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 3 | 19,5 | 6 | 22 | -2,5 | 6,25 |
| 2 | 10,5 | 3 | 3 | 7,5 | 56,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 3 | 19,5 | 6 | 22 | -2,5 | 6,25 |
| 2 | 10,5 | 6 | 22 | 11,5 | 132,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 3 | 19,5 | 6 | 22 | -2,5 | 6,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 3 | 19,5 | 4 | 7 | 12,5 | 156,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 1 | 3,5 | 4 | 7 | -3,5 | 12,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
|
| 
| 620 | |||
|
| r = | 0,611 | |||
Рассчитать коэффициент ранговой корреляции Спирмена по формуле:

а) при отсутствии одинаковых рангов;
 = 1- (6*620)/(24 (242-1) =0,73
= 1- (6*620)/(24 (242-1) =0,73
б) при наличии одинаковых рангов

При наличии одинаковых рангов рассчитать поправки:


где а и b - объем каждой группы одинаковых рангов в ранговых рядах А и В
 =
=  +
+ 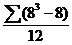 +
+  =142
=142
 =
=  +
+  +
+ 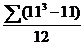 +
+  =132
=132
 =
= 
Сравнив эмпирическое значение 0,611 с критическим в 0,53 для n=24 приходим у опровержению нулевой гипотезы.
Связь между двумя качественными признаками можно оценить, используя выборочный коэффициент ранговой корреляции Кендалла:

R=R1+ R2+ …….Rn-1
Произведем расчет коэффициента ранговой корреляции Кендалла и сравним его значение со значением коэффициента ранговой корреляции Спирмена.
| Симметричные меры | |||||
| Значение | Асимптотическая стдандартная ошибкаa | Прибл. Tb | Прибл. значимость | ||
| Порядковая по порядковой | Тау-b Кендалла | ,622 | ,115 | 4,835 | ,000 |
| Тау-c Кендалла | ,625 | ,129 | 4,835 | ,000 | |
| Кол-во валидных наблюдений | 24 | ||||
| a. Не подразумевая истинность нулевой гипотезы. | |||||
| b. Используется асимптотическая стандартная ошибка в предположении истинности нулевой гипотезы. | |||||
Пример: три арбитра оценили мастерство 10 фигуристов, в итоге были получены три последовательности рангов:
| Ранг арбитра А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранг арбитра В | 3 | 10 | 6 | 2 | 8 | 5 | 7 | 9 | 1 | 4 |
| Ранг арбитра С | 6 | 3 | 1 | 2 | 9 | 4 | 5 | 7 | 10 | 8 |
Выявить два арбитра, оценки которых наиболее согласуются.
r12= -0,16, r13= 0,61, r23= 0,15 – оценки арбитров А и С наиболее согласуются.
Частная корреляция
В то время как линейный коэффициент корреляции — это показатель силы связи, описывающий линейную зависимость между двумя переменными, частный коэффициент корреляции является мерой зависимости между двумя переменными при фиксированных (исключенных) одной или нескольких переменных.
Суть частной корреляции заключается в следующем. Если две переменные коррелируют, всегда можно предположить, что эта корреляция обусловлена влиянием третьей переменной, как общей причины совместной изменчивости первых двух переменных. Для проверки этого предположения достаточно исключить влияние этой третьей переменной и вычислить корреляцию двух переменных без учета влияния третьей переменой (при фиксированных ее значениях). Корреляция, вычисленная таким образом, называется частной.
Например, при исследовании связи между скоростью чтения и зрелостью моральных суждений у детей разного возраста наверняка будет обнаружена корреляция этих двух переменных. Ответ на вопрос, связаны ли они непосредственно, или связь обусловлена возрастом, позволяет дать частная корреляция. Если при фиксированных значениях возраста частная корреляция скорости чтения и зрелости моральных суждений уменьшается, приближаясь к нулю, можно заключить, что связь между этими переменными обусловлена возрастом.
Например частная корреляция позволяет выявить, зависит ли объем продаж от расходов на рекламу, если фиксировать влияние цены (исключить эффект цены) или выявить связь между восприятием качества товаров потребителями с их восприятием цены, если исключить эффект торговой марки. В изучении корреляции между образованием и доходом исключаем эффект интеллекта, предположительно влияющего и на образование, и на доход. Полученная величина будет свидетельствовать о чистом влиянии образования на доход, из которого «вычтена» линейная зависимость образования от интеллекта
В исследовании П. Риттербэнда и Р. Силберстайна изучались студенческие беспорядки 1968—1969 гг. Одна из гипотез заключалась в том, что число нарушений дисциплины и демонстраций протеста в старших классах учебных заведений связано с различиями показателей академической успеваемости учащихся. Корреляция между частотой «политических» беспорядков и средней успеваемостью оказалась отрицательной (хуже успеваемость — больше беспорядков) и статистически значимой (0,36). Однако еще более высокой была корреляция между частотой беспорядков и долей чернокожих учащихся ( 0,54). Исследователи решили проверить, сохранится ли связь между беспорядками и успеваемостью, если статистически проконтролировать влияние расового состава учащихся. Коэффициент частной корреляции частоты беспорядков и успеваемости при контроле расового состава учащихся оказался равным нулю. Исходная корреляция между беспорядками и успеваемостью в данном случае может быть описана причинной моделью «ложной взаимосвязи» наблюдаемые значения этих двух переменных скоррелированы лишь потому, что обе они зависят от третьей переменной — доли чернокожих в общем количестве учащихся. Чернокожие студенты, как заметили исследователи, оказались восприимчивее к предложенным самыми активными «политиканами» образцам участия в политических беспорядках. Кроме того, их успеваемость, помимо всяких политических событий, была устойчиво ниже, чем средняя успеваемость белых.
Простой коэффициент корреляции между двумя переменными полностью описывает линейную зависимость между ними, а частный коэффициент корреляции можно вычислить, зная только эти простые, коэффициенты корреляции и не используя отдельные наблюдения.
Исключить влияние третьей переменной позволяет частный коэффициент корреляции. 
Связь между изучаемыми признаками:
Если коэффициент имеет положительный знак, то связь положительная, при отрицательном знаке - связь отрицательная.
По абсолютному значению коэффициента (от 0 до 1) оцениваем количественную меру связи:
| rxy(z) | 0 | 0,0-0,2 | 0,2-0,5 | 0,5-0,7 | 0,7-0,9 |
| наличие корреляции | корреляция отсутствует | связь очень слабая | связь слабая | связь средняя | связь сильная |
Пример: у группы спортсменов измерили результат в прыжках в длину (X), массу тела (Y) и силу мышц нижних конечностей (Z).Коэффициенты линейной корреляции rxy=0,78, rxz =0,89, ryz=0,95. Выявить "чистую" корреляцию между результатами в прыжках в длину и массой тела, исключая влияние на эту взаимосвязь силы мышц нижних конечностей
частный коэффициент корреляции по формуле:
 =-0,5
=-0,5
полученный отрицательный коэффициент свидетельствует о том, что при прочих равных условиях (одинаковой силе мышц нижних конечностей) спортсмены с большей массой тела прыгали бы хуже.
В случае, когда необходимо вычислить коэффициент корреляции между двумя неметрическими переменными (их нельзя измерить с помощью интервальной или относительной шкалы и они не подчиняются закону нормального распределения) используют два показателя неметрической корреляции: коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла. Для вычисления этих коэффициентов используют ранги, а не абсолютные значения переменных. Оба коэффициента изменяются в диапазоне от минус до плюс единицы.
Коэффициент ранговой корреляции Кендалла целесообразно использовать, когда большинство наблюдений попадает в относительно небольшое число категорий (что приводит к большому количеству связанных рангов). Целесообразно использовать коэффициент ранговой корреляции Спирмена, когда мы имеем относительно большое число категорий (что приводит к небольшому количеству совпадающих рангов).
Пример:в ф. Социальная стратификация выявить, обусловлена ли корреляция между переменными местом проживания (resp) и степенью доверия к средствам СМИ (83_4) влиянием третьей переменной – возраст (q2).
Если рассмотреть корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи при использовании п.м. Анализ/Корреляции/Парные, получаем результаты:
| Корреляции | ||||
| Q83_4. В какой степени Вы доверяете СМИ: | Q68. Сколько книг Вы прочли за последние три месяца? | Q2. полных лет | ||
| Q83_4. В какой степени Вы доверяете СМИ | Корреляция Пирсона | 1 | ,066** | -,025** |
| Знч.(2-сторон) | ,000 | ,002 | ||
| N | 14601 | 14601 | 14601 | |
| Q68. Сколько книг ( Вы прочли за последние три месяца ? | Корреляция Пирсона | ,066** | 1 | -,118** |
| Знч.(2-сторон) | ,000 | ,000 | ||
| N | 14601 | 15200 | 15200 | |
| Q2 полных лет | Корреляция Пирсона | -,025** | -,118** | 1 |
| Знч.(2-сторон) | ,002 | ,000 | ||
| N | 14601 | 15200 | 15200 | |
| **. Корреляция значима на уровне 0.01 (2-сторон.). | ||||
Полученные результаты можно трактовать, таким образом, что доверие к СМИ довольно сильно коррелирует с количеством прочтенных книг (r =0, 66). Количество прочтенных книг коррелирует с возрастом (r =- 0,118), доверие к СМИ также коррелирует с возрастом (r =- 0,25).
Таким образом, возникает подозрение, что возраст является искажающим признаком, виновным в ложной корреляции между доверием к СМИ и числом прочтенных книг. Докажем это путём расчёта частных корреляционных коэффициентов при использовании п.м. Анализ/Корреляции/ Частные, поместив переменную Возраст в исключенные, получаем результаты:
| Корреляции | ||||
| Контрольные переменные | Q83_4. В какой степени Вы доверяете СМ И | Q68. Сколько книг Вы прочли за последние три месяца (? | ||
| Q2. полных лет | Q83_4. В какой степени Вы доверяете СМИ | Корреляция | 1,000 | ,063 |
| Значимость (2-сторон.) | . | ,000 | ||
| ст.св. | 0 | 14598 | ||
| Q68. Сколько книг ( Вы прочли за последние три месяца)? | Корреляция | ,063 | 1,000 | |
| Значимость (2-сторон.) | ,000 | . | ||
| ст.св. | 14598 | 0 | ||
Результаты показывают, что значение коэффициента корреляции незначительно уменьшилось от r =0, 66 до r =0, 63. Можно сделать вывод, что при исключении искажающей переменной Возраст связь между этими переменными частично обусловлена возрастом.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
ЗАДАЧА 1.В фирме провели медицинское обследование, в ходе которого было выявлено, что в течение последнего года у сотрудников понизилось зрение. Сделать выводы о зависимости между полом и выявленным заболеванием при значении уровня значимости в 0,05, вычислив значение хи-квадрат Пирсона (ф. Служащие). Выведите значения ожидаемых частот и сделайте предположение о наличии или отсутствии связи между признаками.
Оцените о наличии или отсутствии связи между признаками по значению к. Пирсона.
| Наличие заболевания | мужчины | женщины |
| Наблюдается | 6 | 41 |
| Не наблюдается | 118 | 137 |
ЗАДАЧА 2.Проверяется эффективность внедрения прививок во время эпидемии гриппа. Сделать выводы об эффективности прививок.
| Наличие заболевания | Прививка сделана | Прививка не сделана |
| Наблюдается | 6 | 180 |
| Не наблюдается | 36 | 120 |
ЗАДАЧА 3.Проведено тестирование школьников на их способность к аналитическому мышлению (тест 1), а также еще три теста – память, логика, абстрактное мышление. Сделать выводы о корреляции между данными первого тестирования и тремя последующими.
| Тест1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Тест-аналитика | 22 | 34 | 56 | 33 | 30 | 48 | 21 | 20 | 36 | 38 | 60 | 45 | 57 | 31 | 54 | 34 | 29 | 37 |
| Тест-память | 21 | 33 | 46 | 33 | 29 | 46 | 20 | 20 | 33 | 32 | 58 | 40 | 50 | 33 | 39 | 33 | 29 | 36 |
| Тест- логика | 14 | 45 | 50 | 36 | 31 | 46 | 19 | 27 | 35 | 37 | 55 | 46 | 51 | 33 | 53 | 33 | 22 | 41 |
| Тест- абстрактное мышление | 10 | 11 | 13 | 13 | 14 | 15 | 9 | 18 | 35 | 20 | 15 | 19 | 18 | 11 | 30 | 12 | 9 | 8 |
ЗАДАЧА 4. Администрация учебного заведения приняла решение повысить уровень оплаты обучения студентов. Среди преподавателей был проведен опрос по поводу выявления их отношения к этому решению. По приведенным ниже данным выявить, существует ли связь между отношением к повышению уровня оплаты и полом преподавателя, а также отношением к этому решению и видом дисциплины, которую читает преподаватель.
| Повышение уровня оплаты | мужчины | женщины |
| Поддерживают | 12 | 8 |
| Не поддерживают | 15 | 12 |
| всего | 27 | 20 |
| Повышение уровня оплаты | Гуманитарные науки | Естественные науки |
| Поддерживают | 6 | 13 |
| Не поддерживают | 14 | 14 |
| всего | 20 | 27 |
ЗАДАЧА 5.Исследователем выдвинута гипотеза о том, что внешняя привлекательность студенток оказывает влияние на уровень их успеваемости. Верна ли эта гипотеза и какова сила и направления связи, если таковая существует?
| Средняя оценка знаний | Внешняя привлекательность | ||
| не привлекательна | умеренно привлекательна | привлекательна | |
| низкая | 7 | 8 | 15 |
| средняя | 10 | 10 | 16 |
| высокая | 8 | 12 | 14 |
| всего | 25 | 30 | 45 |
ЗАДАЧА 6.Представлены данные о среднем времени ожидания приезда кареты скорой помощи в 2010 и 2015 гг. перевести данные в процентные показатели, построить круговые диаграммы, сделать выводы, сравнив данные.
| Среднее время, мин (2010 г.) | Число вызовов | Среднее время, мин (2015 г.) | Число вызовов |
| Менее 5 | 210 | Менее 5 | 250 |
| 6-10 | 375 | 6-10 | 350 |
| 11-15 | 180 | 11-15 | 155 |
| 16-20 | 15 | 16-20 | 95 |
| Более 20 | 35 | Более 20 | 45 |
ОБОБЩАЮЩИЕ ЗАДАЧИ
ЗАДАЧА 1. Для представленных ниже переменных построить распределение частот, выбрать и рассчитать соответствующий показатель распределения и показатель разброса. Написать обобщающую характеристику для каждой переменной
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
| Возраст | 30 | 37 | 42 | 57 | 27 | 24 | 21 | 20 | 55 | 23 | 60 | 68 | 23 | 38 | 33 | 44 | 59 | 31 | 56 |
| Пол | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 1 | 1 | 2 | 2 |
| Отношение к мигрантам | 1 | 1 | 3 | 1 | 2 | 4 | 2 | 3 | 2 | 1 | 2 | 4 | 1 | 2 | 3 | 1 | 3 | 3 | 1 |
| Место проживания | 1 | 1 | 3 | 4 | 2 | 2 | 1 | 1 | 1 | 2 | 3 | 3 | 1 | 2 | 3 | 4 | 4 | 1 | 3 |
| Время жительства | 2 | 2 | 3 | 4 | 1 | 2 | 2 | 1 | 4 | 3 | 4 | 4 | 1 | 3 | 3 | 4 | 4 | 3 | 4 |
Пол – 1 –муж., 2 – ж
Дата добавления: 2018-04-04; просмотров: 2545; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
