При вычислении хи-квадрат для номинальных переменных проверяется нулевая гипотеза о независимости исследуемых переменных, при этом не определяется ни сила, ни направление связи
Вместе со значением хи-квадрат рассчитывается значение р-уровня значимости.
При р>0,05 cчитается, что различия между наблюдаемыми и ожидаемыми частотами незначительны, нулевая гипотеза о независимости переменных принимается и обосновывается вывод о независимости переменных.
При р<0,05 нулевая гипотеза о независимости переменных отклоняется и обосновывается вывод о зависимости переменных.
Пример:
| Таблица сопряженности Пол сотрудника * Категория занятости | ||||||
| Категория занятости | Итого | |||||
| 1 Сотрудник секретариата | 2 Сотрудник среднего звена | 3 Менеджер | ||||
| Пол сотрудника | 1 жен | Частота | 157 | 27 | 74 | 258 |
| Ожидаемая частота | 197,6 | 14,7 | 45,7 | 258,0 | ||
| 2 муж | Частота | 206 | 0 | 10 | 216 | |
| Ожидаемая частота | 165,4 | 12,3 | 38,3 | 216,0 | ||
| Итого | Частота | 363 | 27 | 84 | 474 | |
| Ожидаемая частота | 363,0 | 27,0 | 84,0 | 474,0 | ||
Наблюдаемые частоты отличны от ожидаемых, поэтому предполагаем зависимость между переменными.
| Критерии хи-квадрат | |||||||||||
|
| Знч. Монте-Карло (2-стор.) | Знч. Монте-Карло (1-стор.) | |||||||||
| 99% доверительный интервал | 99% доверительный интервал | ||||||||||
| Значение | ст.св. | Асимпт. значимость (2-стор.) | Знч. | Нижняя граница | Верхняя граница | Знч. | Нижняя граница | Верхняя граница | |||
| Хи-квадрат Пирсона | 79,277a | 2 | ,000 | ,000b | ,000 | ,000 | |||||
| Отношение правдоподобия | 95,463 | 2 | ,000 | ,000b | ,000 | ,000 | |||||
| Точный критерий Фишера | 90,869 | ,000b | ,000 | ,000 | |||||||
| Линейно-линейная связь | 67,463c | 1 | ,000 | ,000b | ,000 | ,000 | ,000b | ,000 | ,000 | ||
| Кол-во валидных наблюдений | 474 | ||||||||||
| a. В 0 (,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 12,30.
| |||||||||||
| b. На основании 10000 случайных таблиц с начальным значением 2000000 датчика случайных чисел. | |||||||||||
| c. Стандартизованная статистика равна -8,214. | |||||||||||
Действительно, р=0,000 – наличие связи.
Так как значение хи-квадрат определяется объемом выборки, сравнение двух значений хи-квадрат, полученных при разных условиях, становится бессмысленным.
К. Пирсон предложил рассечет коэффициента фи с целью более наглядной интерпретации связи
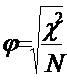
Коэффициент j как изменяется от 0 (независимые переменные) до 1. Однако, если одна из переменных имеет более двух градаций, значение фи может превышать значение в единицу. В этом случае может быть использован к. Крамера, который может принимать значения от единицы (строго связанные переменные) до нуля (для независимых переменных).

k – наименьшее из чисел градаций двух переменных,
N – размер выборки
|
|
|
В примере значение этих коэффициентов также свидетельствует о наличии связи.
| Симметричные меры | ||||||
|
| Знч. Монте-Карло | |||||
| 99% доверительный интервал | ||||||
| Значение | Прибл. значимость | Знч. | Нижняя граница | Верхняя граница | ||
| Номинальная по номинальной | Фи | ,409 | ,000 | ,000a | ,000 | ,000 |
| V Крамера | ,409 | ,000 | ,000a | ,000 | ,000 | |
| Кол-во валидных наблюдений | 474 | |||||
| a. На основании 10000 случайных таблиц с начальным значением 2000000 датчика случайных чисел. | ||||||
Ошибка первого рода – когда нулевая гипотеза отвергается, хотя она верна.
Вероятность допустить ошибку первого рода равна вероятности ошибки р.
Уровень статистической значимости
| Вероятность допустить ошибку первого рода | Значение р | интерпретация |
| 5% | р<0,05 | низший уровень статистической значимости |
| 1% | p<0,01 | достаточный уровень статистической значимости |
| 0,1% | p<0,001 | высокий уровень статистической значимости |
Ошибка второго рода – когда нулевая гипотеза принимается, хотя она ложна.
Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р. Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая. В значительной степени эта вероятность определяется характером исследуемой ситуации.
|
|
|
Чем больше требуемая вероятность, с которой надо избежать ошибочного решения, тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Значение критерия хи-квадрат в значительной степени определяется количеством ячеек таблицы сопряженности и объемом выборки, поэтому сопоставление двух значений хи-квадрат, полученных при разных условиях, становится бессмысленным.
Таблицы сопряженностистроятся через меню Описательные статистики / Таблицы сопряженности.
Диалоговое окно Таблицы сопряженности позволяет определить одну или несколько переменных в состав таблицы, а также осуществить вывод столбиковой диаграммы. Обычно в строки помещают независимую переменную, а в столбцы – зависимую.
Область Слой позволяет вложить одну переменную в состав другой, таким образом, построить таблицу для трех и более переменных.
Например: ф . Служащие.
Определим переменную «пол»– в строки, переменную «зрение» – в столбцы, а переменную «категория занятости» – в слои, а то для каждой категории занятости будут созданы вложенные слои для мужчин и женщин отдельно.
|
|
|
| Таблица сопряженности Пол сотрудника * заболевание * Категория занятости | ||||||
| Категория занятости | заболевание | Итого | ||||
| 1,00 в норме | 2,00 нарушение зрения | |||||
| 1 Сотрудник секретариата | Пол сотрудника | 1 жен | Частота | 45 | 111 | 156 |
| Ожидаемая частота | 57,3 | 98,7 | 156,0 | |||
| % в заболевание | 33,8% | 48,5% | 43,1% | |||
| 2 муж | Частота | 88 | 118 | 206 | ||
| Ожидаемая частота | 75,7 | 130,3 | 206,0 | |||
| % в заболевание | 66,2% | 51,5% | 56,9% | |||
| Итого | Частота | 133 | 229 | 362 | ||
| Ожидаемая частота | 133,0 | 229,0 | 362,0 | |||
| % в заболевание | 100,0% | 100,0% | 100,0% | |||
| 2 Сотрудник среднего звена | Пол сотрудника | 1 жен | Частота | 1 | 18 | 19 |
| Ожидаемая частота | ,7 | 18,3 | 19,0 | |||
| % в заболевание | 100,0% | 69,2% | 70,4% | |||
| 2 муж | Частота | 0 | 8 | 8 | ||
| Ожидаемая частота | ,3 | 7,7 | 8,0 | |||
| % в заболевание | ,0% | 30,8% | 29,6% | |||
| Итого | Частота | 1 | 26 | 27 | ||
| Ожидаемая частота | 1,0 | 26,0 | 27,0 | |||
| % в заболевание | 100,0% | 100,0% | 100,0% | |||
| 3 Менеджер | Пол сотрудника | 1 жен | Частота | 54 | 20 | 74 |
| Ожидаемая частота | 56,4 | 17,6 | 74,0 | |||
| % в заболевание | 84,4% | 100,0% | 88,1% | |||
| 2 муж | Частота | 10 | 0 | 10 | ||
| Ожидаемая частота | 7,6 | 2,4 | 10,0 | |||
| % в заболевание | 15,6% | ,0% | 11,9% | |||
| Итого | Частота | 64 | 20 | 84 | ||
| Ожидаемая частота | 64,0 | 20,0 | 84,0 | |||
| % в заболевание | 100,0% | 100,0% | 100,0% | |||
Значение критерия рассчитывается отдельно для каждого слоя
| Критерии хи-квадратh | |||||||
| Категория занятости | Значение | ст.св. | Асимпт. значимость (2-стор.) | Точная значимость (2-стор.) | Точная значимость (1-стор.) | Вероятность в точке | |
| 1 Сотрудник секретариата | Хи-квадрат Пирсона | 7,350a | 1 | ,007 | ,008 | ,004 | |
| Поправка на непрерывностьb | 6,766 | 1 | ,009 | ||||
| Отношение правдоподобия | 7,441 | 1 | ,006 | ,008 | ,004 | ||
| Точный критерий Фишера | ,008 | ,004 | |||||
| Линейно-линейная связь | 7,330c | 1 | ,007 | ,008 | ,004 | ,002 | |
| Кол-во валидных наблюдений | 362 | ||||||
| 2 Сотрудник среднего звена | Хи-квадрат Пирсона | ,437d | 1 | ,508 | 1,000 | ,704 | |
| Поправка на непрерывностьb | ,000 | 1 | 1,000 | ||||
| Отношение правдоподобия | ,719 | 1 | ,397 | 1,000 | ,704 | ||
| Точный критерий Фишера | 1,000 | ,704 | |||||
| Линейно-линейная связь | ,421e | 1 | ,516 | 1,000 | ,704 | ,704 | |
| Кол-во валидных наблюдений | 27 | ||||||
| 3 Менеджер | Хи-квадрат Пирсона | 3,547f | 1 | ,060 | ,108 | ,055 | |
| Поправка на непрерывностьb | 2,214 | 1 | ,137 | ||||
| Отношение правдоподобия | 5,849 | 1 | ,016 | ,065 | ,055 | ||
| Точный критерий Фишера | ,108 | ,055 | |||||
| Линейно-линейная связь | 3,505g | 1 | ,061 | ,108 | ,055 | ,055 | |
| Кол-во валидных наблюдений | 84 | ||||||
| a. В 0 (,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 57,31. | |||||||
| b. Вычисляется только для таблицы 2x2. | |||||||
| c. Стандартизованная статистика равна -2,707. | |||||||
| d. В 2 (50,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна ,30. | |||||||
| e. Стандартизованная статистика равна ,649. | |||||||
| f. В 1 (25,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 2,38. | |||||||
| g. Стандартизованная статистика равна -1,872. | |||||||
| h. Для таблицы сопряженности 2x2 вместо результатов Монте-Карло даются точные результаты. | |||||||
В этом случае столбиковые диаграммы выводятся отдельно для каждого слоя.

Дата добавления: 2018-04-04; просмотров: 272; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
