Данные/Отобрать наблюдения/Случайная выборка/Подвыборка
Можно выбрать один из следующих способов определения объема выборки:
Примерно – процентное значение, создание случайной выборки с объемом, приблизительно соответствующим указанному проценту наблюдений.
Точно – точное количество наблюдений в случайной выборке.
Для каждой случайной выборки генератор случайных чисел SPSS использует новое начальное значение – создание новых выборок наблюдений, отличных от прежних.
Если требуется, чтобы случайная выборка повторялась, надо задать начальное значение самостоятельно, для чего нужно установить начальное положение генератора случайных чисел.
Сортировка наблюдений
Данные можно ранжировать в соответствии со значениями одной или нескольких переменных, используя команду
Данные/Сортировать наблюдения
Возможна сортировка в порядке возрастания или в порядке убывания значения переменной сортировки. Команде соответствует синтаксис:
SORT CASES BY ИМЯ ПЕРЕМЕННОЙ (A)
– сортировка по возрастанию значений
SORT CASES BY ИМЯ ПЕРЕМЕННОЙ (D)
Например, сортировка по убыванию значений калорийности:
SORT CASES BY калории(D).
Разделение наблюдений на группы
Группа представляет собой определенное количество наблюдений с одинаковыми значениями признаков.
Чтобы можно было производить обработку по группам, файл должен быть отсортирован по группирующим переменным. Такой переменной может быть, например, переменная Пол. В этом случае все переменные со значением признака 2 (женский) образуют одну группу, а все переменные со значением признака 1 (мужской) — другую группу. С каждой группой можно проводить определенные операции, например, выполнять частотный анализ, который проводится раздельно для признаков мужской и женский.
|
|
|
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.
Задача 1. В файле Служащие.sav выполнить частотный анализ по переменной jobcat (категория занятости) отдельно для мужчин и женщин
1. Пример: Откройте файл Служащие.sav
2. В меню Данные/Расщепить файл/Сравнить группы/Группы образуются по задать переменную gender
SORT CASES BY gender.
Задача 2. В файле Служащие.sav провести частотный анализ по переменной «зарплата в настоящее время». В качестве группировочного признака выбрать категорию занятости,
Задача 3. В файле Выборы.sav подсчитать количество мужчин и женщин, которые не пойдут на выборы.
Задача 4. В файле Выборы.sav подсчитать количество респондентов, которые не пойдут на выборы. В качестве группировочного признака выбрать уровень образования,
Задача 5. В файле Выборы.sav организовать новую переменную «Возрастные группы», определив возраст респондентов в группы 18-25, 26-40, 41-60, старше 61 года. Расщепить файл по новой переменной и осуществить частотный анализ по переменной «Оцените материальное положение Вашей семьи». Сделать выводы.
|
|
|
Часть 4. Понятие корреляции
Общее представление о корреляции
Исследуя общество, экономику, необходимо учитывать взаимосвязь наблюдаемых процессов и явлений. Оценка наиболее существенных факторов, а также воздействия одних факторов на другие является одной из основных задач статистики.
Статистические распределения характеризуются вариацией в величине признака, что можно объяснить зависимостью этой величины от условий ее формирования и окружающих условий.
Вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующих исследуемую совокупность единиц.
Пример: уровень дохода респондентов зависит от уровня образования, занятости в различных сферах экономики, брачного состояния, др.
Признаки, выступающие в виде факторов, обуславливающих изменение других признаков, называют факторными признаками.
Признаки, являющиеся результатом влияния факторных признаков, называют результативными признаками.
|
|
|
Пример: уровень дохода – результативный признак, занятость – факторный признак.
В качестве двух самых общих видов выделяют функциональную (полную) и корреляционную (неполную) связи.
Функциональная связь характеризуется полным соответствием между изменением величины факторного признака и изменением результативной величины, когда каждому изменению величины факторного признака соответствуют определенные значения результативного признака.
Пример: прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции.
Корреляционная связь не наблюдается полное соответствие между изменением величины факторного признака и изменением результативной величины. Такая связь проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной, что можно объяснить сложностью взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
|
|
|
Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно.
Пример: связь между урожайностью и количеством внесенных удобрений (для каждого участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов – погода, состояние почвы, которые и формируют конечный результат). Однако в среднем такая связь наблюдается – увеличение массы внесенных удобрений ведет к росту урожайности.
Одновременное воздействие на изучаемый признак большого количества факторов приводит к тому, что одному значению признак-фактора соответствует целое распределение значений результативного признака.
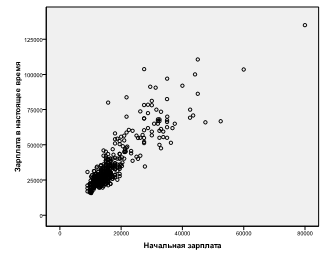
По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные – множественной.
Различают также непосредственные, косвенные и ложные связи. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ.
Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.
Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.
Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы – параметрические – и принято называть корреляционными.
Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений.
Корреляция определяется значением коэффициента корреляции (r Пирсона) – это статистический показатель вероятностной связи между двумя переменными, измеренными в количественной шкале.
Расчеты критериев взаимосвязи основывается на формировании парных значений из зависимых выборок.
Корреляция представляет собой величину, заключенную в пределах от –1 до +1, где 0 означает отсутствие связи.
| Значение | Интерпретация корреляции |
| до 0,2 | Очень слабая |
| до 0,5 | Слабая |
| до 0,7 | Средняя |
| до 0,9 | Высокая |
| Свыше до 0,9 | Очень высокая |
Строгая положительная корреляция r = 1 – значения одной переменной однозначно определяются значениями другой переменной (с возрастанием значений одной переменной значения другой переменной также возрастают). Строгая корреляция является математической абстракцией и практически не встречается в реальных исследованиях.
Пример: соответствие между временем пути и пройденным расстоянием при неизменной скорости.
Пример: соответствие между стажем работы и уровнем заработной платы.
Положительная корреляция 0 < r < 1 – если значения одной переменной возрастают, то значения другой имеют тенденцию к возрастанию.
Пример: зависимость между ростом и весом человека (r = 0,83 – сильная положительная корреляция).
Пример: зависимость между способностью человека к сочувствию и реальной помощью, которую он оказывает (r = 0,12 – слабая положительная корреляция).
Отсутствие корреляции r = 0 – значения переменных никак не связаны друг с другом.
Пример: зависимость между доходом респондента и результатами обучения.
Отрицательная корреляция –1 < r < 0 – когда значения одной переменной возрастают, то значения другой имеют тенденцию к убыванию.
Пример: зависимость между агрессивностью человека по отношению к своему другу и помощью, которую он ему оказывает (r = –0,13 – слабая отрицательная корреляция).
Пример: зависимость между нервной возбудимостью человека и его эмоциональной уравновешенностью (r = –0,73 – сильная отрицательная корреляция).
Строгая отрицательная корреляция r = –1 как и строгая положительная корреляция, является абстракцией и не находит отражения в практических исследованиях.
Между переменными может наблюдаться функциональная связь, при которой каждому значению одной переменной соответствует определенное значение другой переменной.
Крайние значения к. Пирсона соответствуют линейной функциональной связи между двумя переменными,
Вероятностная связь между переменными характеризуется тем, что каждому значению одной переменной соответствует множество значений другой переменной.
Пример: связь между ростом и весом людей (один и тот же рост может быть у людей разного веса, как и наоборот).
Понятия «корреляция» и «двумерная корреляция» (как «корреляция между двумя переменными») часто употребляются как синонимы.
Коэффициент Пирсона предназначен для оценки связи между двумя переменными, измеренными в количественной шкале, распределение которых соответствует нормальному. Вычисление этого коэффициента дает достаточно точные результаты и в случаях анормальных распределений.
Дата добавления: 2018-04-04; просмотров: 276; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
