Формула для вычисления дисперсии
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
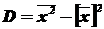
Групповая, внутри групповая, межгрупповая и общая дисперсии
Допустим, что все значения количественного признака X разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю (см. § 6) и дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
,
где ni - частота значения хi; j - номер группы;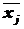 
- групповая средняя группы j; 
- объем группы j.
Зная дисперсию каждой группы, можно найти их среднюю арифметическую.
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
где Nj — объем группы j;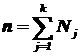 
- объем всей совокупности.
Зная групповые средние и общую среднюю, можно найти дисперсию групповых средних относительно общей средней.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
,
где 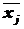- групповая средняя группы j; Nj—объем группы j; 
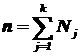- общая средняя; - объем всей совокупности.
Теперь целесообразно ввести специальный термин для дисперсии всей совокупности.
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
,
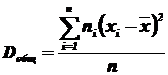где ni - частота значения хi ; - общая средняя; п — объем всей совокупности.
|
|
|
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
Оценка генеральной дисперсии по исправленной выборочной
Можно показать, что выборчная дисперсия является смещенной оценкой генеральной дисперсии:
.
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить Dв на дробь п/(п—1). Сделав это, получим исправленную дисперсию, которую обычно обозначают через s2:
Исправленная дисперсия является несмещенной и состоятельной оценкой генеральной дисперсии.
Для оценки среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение (стандартная ошибка), которое равно квадратному корню из исправленной дисперсии:
Точность оценки, доверительная вероятность (надежность).
Доверительный интервал
Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, - точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
|
|
|
Интервальной оценкой называют интервал, в который оцениваемая величина попадает с заданной надежностью (доверительной вероятностью) g. Интервальная оценка определяется соотношением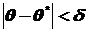 
. Положительное число d характеризует точность оценки. Величина d определяется из следующего соотношения:
.
d - точность (или погрешность) оценки, d также называют полушириной доверительного интервала. Очевидно, что величина d зависит от надежности оценки g . Для того, чтобы интервальная оценка имела смысл, величина g должна быть близка к 1.
Заменив неравенство 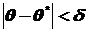равносильным ему двойным неравенством 
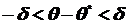или, имеем
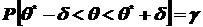
Это соотношение следует понимать так: вероятность того, что интервал 
заключает в себе (покрывает) неизвестный параметр q, равна g.
Доверительным называют интервал , который покрывает неизвестный параметр с заданной надежностью g.
Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.
Дата добавления: 2018-04-04; просмотров: 431; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!