СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ
РАСПРЕДЕЛЕНИЯ
ОЦЕНКА ПАРАМАТРОВ РАСПРЕДЕЛЕНИЯ
Пусть по результатам экспериментальных данных требуется оценить некоторый количественный признак генеральной совокупности. Будем называть выборочной статистикой любую величину, полученную в результате обработки данных эксперимента.
Пусть имеется выборка объема n некоторого параметра q : q1 , q2 , … , qn . Для другой выборки объема n будет получен другой набор значений параметра q : q1 , q2 , … , qn . Поэтому любая выборочная статистика является случайной величиной. Имеют место следующие определения математической статистики.
Определение. Точечной оценкой параметра x называется его приближенное значение 
, полученное в результате обработки выборки.
На основании вышеизложенного является случайной величиной.
Определение. Оценка параметра x называется несмещенной, если математическое ожидание оценки совпадает с оцениваемым параметром: M( ) = x .
Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.
Определение. Оценка параметра x называется состоятельной, если при увеличении объема выборки n для любого e ³ 0 вероятность отклонения оценки от параметра x на величину, меньшую e, равна 1:
Целесообразность использования несмещенных и состоятельных оценок объясняется тем, что на разных выборках одного объема полученные оценки группируются около оцениваемой величины, и можно добиться сколь угодно высокой точности оценивания за счет увеличения объема выборки.
|
|
|
Пусть по результатам эксперимента требуется оценить математическое ожидание генеральной совокупности. Можно показать, что несмещенной и состоятельной оценкой математического ожидания а оцениваемого признака q является выборочная средняя:
,
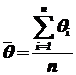где qi -варианты выборки выходного параметра q .
Состоятельность выборочной средней означает, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит свойство устойчивости выборочных средних.
Групповая и общая средние
Допустим, что все значения количественного признака X разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.
Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.
Общей средней 
называют среднее арифметическое значений признака, принадлежащих всей совокупности.
Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.
|
|
|
Выборочная дисперсия
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 
, вводят сводную характеристику - выборочную дисперсию.
Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения :
.
Дата добавления: 2018-04-04; просмотров: 252; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!