Построение взаимно перпендикулярных плоскостей

Чтобы построить плоскость, перпендикулярную заданной, её нужно провести через перпендикуляр к этой плоскости.

Пример1:

Плоскость задана треугольником АВС. Через прямую МN провести плоскость, перпендикулярную треугольнику АВС (рис.52).

Рис. 52 Построение плоскости, перпендикулярной заданной

Мы знаем, что плоскость может быть задана пересекающимися прямыми, поэтому для построения плоскости, перпендикулярной заданной из конца заданного отрезка (а именно из точки N) восстановим перпендикуляр к заданной плоскости (треугольнику АВС). Искомая плоскость будет определяться прямой МN и перпендикуляром к плоскости треугольника. Для проведения этого перпендикуляра в плоскости треугольника строим горизонталь h и фронталь f. Затем из горизонтальной проекции точки N' проводим N'F' перпендикулярно горизонтальной проекции горизонтали h'. А из фронтальной проекции точки N" проводим N"F" перпендикулярно фронтальной проекции фронтали f".Тогда NF – перпендикулярен к плоскости АВС. Плоскость, заданная пересекающимися прямыми МN и NF, перпендикулярна плоскости треугольника АВС, так как проходит через перпендикуляр к нему.

Пример 2:

Плоскость α задана следами (рис.52). Через точку А провести плоскость β, перпендикулярную α.

Рис. 53 Построение следов плоскости, перпендикулярной заданной

Через точку А проводим прямую, перпендикулярную заданной плоскости α. Для этого из горизонтальной проекции точки А' восстанавливаем перпендикуляр к горизонтальному следу плоскости h_0α, а из фронтальной проекции точки А" – к фронтальному f_0α. Чтобы искомая плоскость β была перпендикулярна заданной плоскости α, она должна проходить через восстановленный перпендикуляр. Находим горизонтальный Н и фронтальный F следы перпендикуляра. Выбрав произвольным образом (т.к. через прямую можно провести бесконечное множество плоскостей) точку схода следов Х_0β, строим фронтальный след плоскости β – f_0β, проведя его через F и Х_0β.Горизонтальный след h_0β получим соединив Х_0β и Н. Плоскость β перпендикулярна заданной плоскости α, т.к. проходит через перпендикуляр к плоскости.

Способ перемены плоскостей проекций

Сущность способа перемены плоскостей проекций заключается в том, что положение точек, плоских фигур, поверхностей в пространстве остаётся неизменным, а система плоскостей проекций ₁, ₂ дополняется плоскостями, образующими с ₁ или ₂(или между собой) системы двух взаимно перпендикулярных плоскостей. Например, плоскость ₄ перпендикулярна плоскости ₁( на рис.54,55).

Нахождение проекции точки А в этом случае представлено на рис.54.

Рис. 54 Способ перемены плоскостей проекций

Сохраняющаяся А' и новая А^IV проекции точки связаны линией проекционной связи, перпендикулярной к новой оси проекций ₁/ ₄ . На этой линии связи от новой оси откладывается отрезок равный расстоянию от заменяемой проекции А" до заменяемой оси Х.

Каждая новая система плоскостей выбирается так, чтобы получилось положение наиболее удобное для требуемого построения.

Часто бывает достаточно введение только одной дополнительной плоскости ₄, перпендикулярной плоскости ₁ или ₂.

Иногда вводят несколько дополнительных плоскостей проекций, например: плоскость ₄, перпендикулярную плоскости ₂, затем плоскость ₅, перпендикулярную плоскости ₄. При этом плоскость ₅ оказывается плоскостью общего положения в основной системе плоскостей ₁, ₂.

Рис.55 Проекция точки на плоскость ₄

Метод перемены плоскостей проекций позволяет решить целый ряд позиционных задач:

1) Определение натуральной величины отрезка.

Мы знаем, что прямая проецируется в свою натуральную величину в том случае, когда она расположена параллельно соответствующей плоскости проекций. Следовательно, нам необходимо расположить новую плоскость проекций параллельно заданной прямой общего положения.

Для этого вводят новую плоскость проекции ₄, перпендикулярную плоскости ₁ (рис.56), а новую ось ₁/ ₄располагают параллельно горизонтальной проекции отрезка А^IB^I. Таким образом прямая АВ становится параллельной по отношению к плоскости _{4 ,} а следовательно ее проекция на эту плоскость А^IVB^IV будет представлять собой истинную длину отрезка, угол α – угол наклона АВ к плоскости ₁.

Рис.56 Определение натуральной величины отрезка

2) Преобразование плоскости общего положения в плоскость проецирующую.

На рисунке 57 плоскость общего положения α задана следами. Мы знаем, что у проецирующих плоскостей один из следов перпендикулярен оси, поэтому новую ось ₁/ ₄ проводим перпендикулярно горизонтальному (как в данном примере), либо – фронтальному следу заданной плоскости α. Угол φ определяет угол наклона заданной плоскости к горизонтальной плоскости проекций.

Если плоскость задана треугольником, то для преобразования её в проецирующую новую ось ₁/ ₄ проводят перпендикулярно горизонтальной проекции горизонтали (рис.58) либо перпендикулярно фронтальной проекции фронтали.

ᵩ

Рис.57 Преобразование плоскости в проецирующую

3) Нахождение натуральной величины треугольника АВС

Треугольник спроецируется в натуральную величину в том случае, если он будет располагаться параллельно соответствующей плоскости проекций. Для решения этой задачи замену плоскостей проекций необходимо выполнять дважды: первый раз новую плоскость проекций ₄ расположим перпендикулярно плоскости треугольника. Для этого в плоскости треугольника проведем горизонталь h. Фронтальную проекцию горизонтали h” проводим параллельно оси х, а положение горизонтальной проекции горизонтали h’ находим по двум точкам (АD), которые лежат в треугольнике. Ось ₁/ ₄ располагается перпендикулярно горизонтальной проекции горизонтали h’. Треугольник проецируется на плоскость ₄в прямую линию, потому что он перпендикулярен ей (проекция А^IVB^IVС^IV).

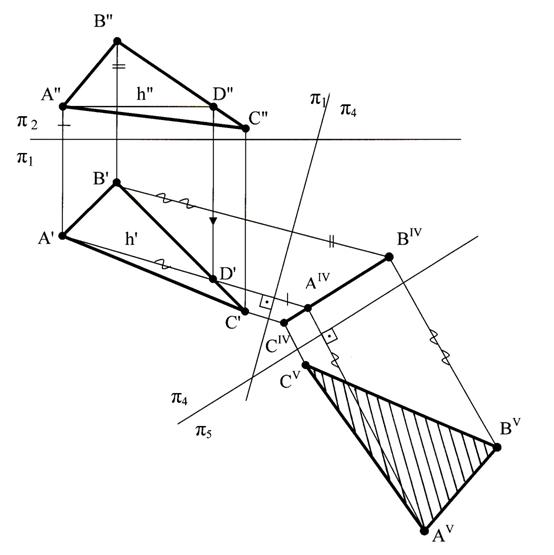
Рис.58 Определение натуральной величины треугольника

Второй раз новую плоскость ₅ расположим параллельно плоскости треугольника. Для этого новую ось ₄/ ₅ и, расположим параллельно проекции треугольника на плоскости ₄ (А^IV,B^IV, С^IV). Найдём проекцию треугольника на плоскость ₅ (А^VB^V С^V). Эта проекция и будет представлять собой натуральную величину треугольника АВС.

4) Определение расстояния между двумя параллельными прямыми АВ и СД .

Потребуется дважды проводить перемену плоскостей проекций.

Рис. 59 Определение расстояния между параллельными прямыми

Вначале ось ₁/ ₄ располагают параллельно одной из проекций прямых, например горизонтальной. Вторую перемену плоскостей проекций проводят таким образом, чтобы прямые спроецировались в точки, т.е. ось ₄/ ₅ располагают перпендикулярно проекциям А^IVB^IV и С^IVD^IV. Тогда расстояние между точкамиА^VB^V и С^VD^V определит расстояние между прямыми АВ и СD в пространстве.

5) Определение расстояние от точки до плоскости.

Для этого заданную плоскость общего положения α нужно преобразовать в проецирующую. А также найти проекцию точки К в новой системе плоскостей проекций ₁/ ₄(К^IV) (рис.60).

Рис.60 Определение расстояния от точки до плоскости

Поскольку кратчайшим расстоянием от точки до плоскости является перпендикуляр, то опустив из проекции точки К^IV перпендикуляр на след 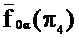, получим натуральную величину расстояния от точки К до плоскости α.

Рассмотренные в данной работе примеры демонстрируют лишь часть геометрических задач, которые позволяет решать способ перемены плоскостей проекций.

Способ вращения

В способе вращения каждая точка перемещается вокруг неподвижной прямой, называемой осью вращения, в плоскости, перпендикулярной оси вращения. Эта плоскость называется плоскостью вращения. Каждая точка вращаемой фигуры перемещается по окружности, центр которой находится в точке пересечения оси с плоскостью вращения, центре вращения. Радиус окружности равен расстоянию от вращаемой точки до центра окружности. Поскольку ось вращения является неподвижной прямой, то все точки, находящиеся на ней неподвижны, в том числе и точки, принадлежащие вращаемой фигуре.

Рис.61 Определение натуральной длины отрезка.

Ось вращения удобно располагать перпендикулярно одной из плоскостей проекций, при этом построения проще. Так, на рисунке 61 решена задача определения натуральной величины отрезка методом вращения, при этом ось вращения расположена перпендикулярно по отношению к фронтальной плоскости проекций ₂ (поэтому проецируется на нее в точку O”) и проходит через один из концов отрезка, а именно точку А (поэтому точка неподвижна). Для того, чтобы найти натуральную длину отрезка АВ повернем его вокруг оси О до положения параллельности плоскости _1,т.е. его фронтальная проекция должна быть параллельна оси Х. Тогда горизонтальная проекция А^lB^l будет представлять собой натуральную величину отрезка. Горизонтальная проекция точки B^l переместится по перпендикуляру к горизонтальной проекции оси вращения O^l.

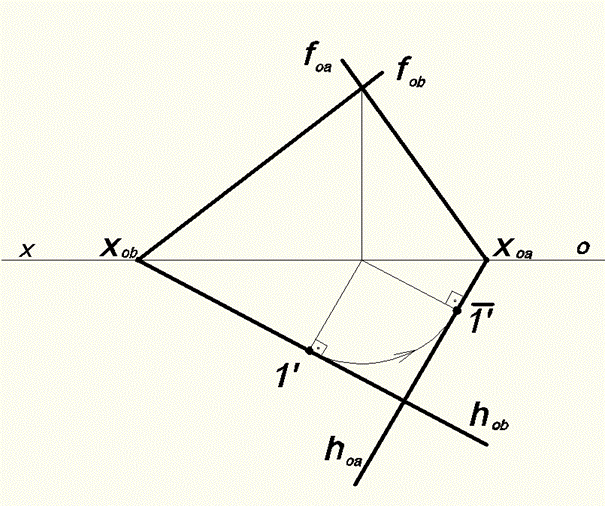
Рис. 62 Поворот плоскости на заданный угол.

На рисунке 62 решена задача поворота плоскости, заданной следами вокруг оси на заданный угол против часовой стрелки. Ось вращения расположена перпендикулярно горизонтальной плоскости проекций ₁,

А также принадлежит фронтальной плоскости проекций _2. Точка, в которой фронтальный след плоскости пересекает ось вращения остается неподвижной. Точка на горизонтальном следе перемещается по радиусу вращения на заданный угол. Горизонтальный след плоскости после поворота остается перпендикулярным по отношению к радиусу вращения, и в пересечении с осью OХ определяет положение точки схода следов Х_0α.

Рис.63 Определение натуральной величины треугольника.

Способом вращения также можно определить натуральную величину многоугольника. На рисунке 63 показано определение натуральной величины треугольника АВС вращением его вокруг горизонтали h. Построение начинается с того, что в плоскости треугольника проводят горизонталь (фронтальная проекция горизонтали h^ll располагается параллельно оси OХ, а положение горизонтальной проекции горизонтали h^l находят по двум точкам (С и 1), общим для горизонтали и треугольника). Точка С будет неподвижной, так как находится на оси вращения (горизонтали). Точки B^l и А^l будут перемещаться по перпендикуляру к оси вращения. Истинную величину радиуса вращения точки B^l найдем способом прямоугольного треугольника. Для определения положения после поворота точки А^l используем тот факт, что точка 1^l неподвижна, так как лежит на оси вращения, а положение точки B^l после поворота уже определено. Проведя прямую через точку B^l и точку 1^l до пересечения с перпендикуляром из А^l к оси вращения, получим положение точки А после поворота. Таким образом, получим натуральную величину треугольника АВС (заштрихован).

Способ совмещения

Частным случаем способа вращения является способ совмещения, когда в качестве оси вращения принимают один из следов плоскости, и поворачивают ее вокруг оси до совмещения с плоскостью проекций. На рисунке 64 в качестве оси вращения принят горизонтальный след плоскости h₀_.На фронтальном следе выбирается произвольная точка (в данном случае N). Ее горизонтальная проекция N^l будет находиться на оси Х, так как фронтальный след, а следовательно и точка на нем принадлежат _2. Точка N^l перемещается по перпендикуляру к оси вращения (т.е. к h₀). Центр вращения точки N^ll находится в точке схода следов плоскости. Положение точки N, совмещенное с ₁ определится при пересечении перпендикуляра с дугой вращения. Совмещенное положение фронтального следа определим соединив N с точкой схода следов плоскости.

Рассмотрим следующую задачу (рис. 65): в плоскости общего положения α лежит отрезок АВ. Нужно определить его натуральную величину методом совмещения, достроить до правильного треугольника и найти горизонтальную и фронтальную проекции построенной точки С.

Рис. 64 Определение положения плоскости после совмещения

В качестве оси вращения принимаем горизонтальный след плоскости h₀и поворачиваем плоскость до совмещения с ₁ в указанном на рисунке направлении. Отрезок АВ принадлежит заданной плоскости, так как точки А и В лежат на горизонталях плоскости. Чтобы найти положение отрезка АВ в совмещенном положении, из горизонтальных проекций концов отрезка A^l и B^l восстанавливаем перпендикуляры к оси вращения (h₀). Все точки, лежащие на фронтальном следе, переместятся вместе с ним в _1. Приняв совмещенное положение отрезка АВ за сторону правильного треугольника, достроим треугольник с помощью циркуля. Горизонтальную и фронтальную проекции точки С найдем выполняя построения в обратном порядке.

Рис. 65 Определение натуральной величины треугольника, лежащегов плоскости общего положения.

Если плоскость занимает частное положение в пространстве, например профильно-проецирующая, то построение выполняется так, как показано на рисунке 66. В качестве оси вращение принят горизонтальный след плоскости h₀_. Направление вращения указано на чертеже. Отрезок АВ лежит в плоскости, так как его следы лежат на одноименных следах

Рис.66 Определение натуральной величины треугольника, лежащего в профильно-проецирующей плоскости.

плоскости. Поскольку осью вращения является горизонтальный след плоскости h₀, а ось вращения неподвижна, то и лежащий на нем горизонтальный след прямой Н остается неподвижным. Фронтальный же след прямой F переместятся вместе с фронтальным следом плоскости f_0α.Получив совмещенное с ₁ положение отрезка АВ, достраиваем его до правильного треугольника (приняв его за сторону). Получим точку С. Для того, чтобы найти горизонтальную C^lи фронтальную C^ll проекции точки, проведем через нее прямую, принадлежащую плоскости, найдем следы прямой Н₁ и F₁, построим горизонтальную и фронтальную проекции прямой. По линии связи из точки С определим С^l (она лежит на горизонтальной проекции прямой) и C^ll (лежит на фронтальной проекции прямой).

Дата добавления: 2018-02-28; просмотров: 6145; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 6 789 Следующая ⇒

Мы поможем в написании ваших работ!