Определение натуральной величины отрезка методом прямоугольного треугольника
Проекция отрезка прямой общего положения всегда меньше его натуральной величины. Но имея проекции отрезка прямой, можно определить какую он на самом деле имеет длину и как расположен в пространстве. Способов определения много, это способ замены плоскостей проекций, способ вращения, способ совмещения (частный случай способа вращения) и т.д. На данном этапе изучения начертательной геометрии, когда мы обладаем еще не большим количеством информации по этому предмету, рассмотрим способ прямоугольного треугольника.
Предположим, что в пространстве имеется отрезок общего положения АВ (рис. 21).
Рис. 21. Метод прямоугольного треугольника
в аксонометрической проекции
Опустив из точек А и В перпендикуляры на плоскость проекций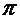 
0, найдем его проекцию на эту плоскость А0В0. Выполнив дополнительное несложное построение, получим прямоугольный треугольник АВ1, у которого гипотенуза является истинной величиной отрезка, один из катетов (А1) равен проекции отрезка на плоскость 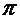0, а второй (В1) равен разности расстояний концов отрезка от плоскости проекций. Таким образом, для того чтобы найти истинную величину отрезка прямой необходимо построить прямоугольный треугольник, один из катетов которого является его проекцией, а второй – разностью расстояний от концов отрезка до соответствующей плоскости проекций. Гипотенуза представляет собой натуральную величину.
|
|
|
Угол α между прямой и плоскостью проекций 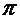0 определяется как угол, составленный прямой с её проекцией на этой плоскости.
Предположим, на эпюре (рис. 22) задана прямая общего положения АВ, своими проекциями А'В' – горизонтальной и А"В" – фронтальной.
Для определения натуральной величины этого отрезка построим прямоугольный треугольник А'В'1, приняв за один из катетов горизонтальную проекцию прямой А'В', в качестве другого величину ∆Z – разность расстояний концов отрезка до горизонтальной плоскости проекций 
1. Тогда, гипотенуза этого треугольника В'1 будет представлять собой натуральную величину отрезка. Угол α – угол наклона прямой АВ к горизонтальной плоскости проекций 1.
Рис. 22. Определение натуральной величины отрезка AB
Аналогичное построение выполнено на фронтальной проекции. Разность расстояний концов отрезка до плоскости 2 определит величина ∆у. Угол β – угол между прямой и фронтальной плоскостью проекций.
Если прямая расположена параллельно какой-либо плоскости проекций, то она спроецируется на нее в натуральную величину.
Проекция плоскости. Следы плоскости
Положение плоскости в пространстве однозначно определяется тремя точками, а в соответствии с этим на эпюре она может быть может быть задана следующим образом (рис.23):
|
|
|
а) проекциями трёх точек, не лежащих на одной прямой;
б) проекциями прямой и точки, не лежащей на прямой;
в) проекциями пересекающихся прямых;
г) проекциями параллельных прямых;
д) следами.
а) б)
в) г)
Рис 23. Задание плоскости на эпюре: а) проекциями трёх точек;
б) проекциями прямой и точки вне прямой; в) проекциями пересекающихся прямых; г) проекциями параллельных прямых
Следы плоскости
Наиболее наглядный способ задания плоскости - следами.
Следы плоскости– это линии, по которым плоскость пересекается с плоскостями проекций. Соответственно у плоскости общего положения (это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций) имеется три следа – горизонтальный, фронтальный и профильный. На чертеже они обозначаются следующим образом: h0 
- горизонтальный след плоскости; f0 - фронтальный и p0 - профильный (рис.24).
|
|
|
а)
| б)
 
|
| Рис. 24. Следы плоскости общего положения: а) в аксонометрической проекции; б) на эпюре
| |
Плоскость, заданную любым из перечисленных выше способов, можно преобразовать в плоскость, заданную следами.
Предположим, плоскость β задана пересекающимися прямыми (рис.25). Для построения прямой, по которой плоскость β пересечет горизонтальную плоскость проекций 1 (т.е. горизонтального следа плоскости h0β), достаточно найти две точки, которые одновременно принадлежали бы плоскости β и плоскости 1. Такими точками будут горизонтальные следы прямых m и n, соответственно Н m , Нn.
Рис. 25. Преобразование плоскости, заданной пересекающимися прямыми, в плоскость, заданную следами
Соединив точки Нm и Нn получим горизонтальный след плоскости h0β. Для построения фронтального следа плоскости найдём фронтальный след прямой m - Fm и фронтальный след прямой n - Fn. Соединив полученные точки (Fm и Fn), получим фронтальный след плоскости f0β.
х0β – точка пересечения следов (f0 и f0β ) на оси Х, называемая точкой схода следов.
Угол между следами на чертеже не равен углу между следами в пространстве ( это видно из рассмотрения трёхгранного угла на рис.24 а) и б)).
|
|
|
Плоскости частного положения
Наряду с плоскостями общего положения существуют плоскости частного положения, которые располагаются перпендикулярно к одной из плоскостей проекций (проецирующие) либо к двум плоскостям проекций (тогда по отношению к третьей плоскости проекций они параллельны).
Если плоскость перпендикулярна к одной из плоскостей проекций, то возможны три случая ее положения.
Горизонтально-проецирующая плоскость– это плоскость перпендикулярная к горизонтальной плоскости проекций.
На рис. 26 дан пример изображения горизонтально-проецирующей плоскости: а) аксонометрическое изображение в системе 1, 2, 3; б) чертёж (эпюр Монжа) в системе 1, 2, 3, где угол φ – угол между плоскостью β и плоскостью проекций 2.
Если в горизонтально-проецирующей плоскости расположена точка, то её горизонтальная проекция должна быть на горизонтальном следе плоскости ( (∙) А' Є h0β ). Это относится к любой системе точек, расположенных в горизонтально-проецирующей плоскости, будь то прямая линия или плоская фигура.
| а) | 
| б) | 
|
|
Рис. 26. Горизонтально-проецирующая плоскость: а) аксонометрическое изображение, б) эпюр | |||
Фронтально-проецирующая плоскость– это плоскость, перпендикулярная фронтальной плоскости проекций.
На рис.27 дан пример её изображения: а) аксонометрическое изображение в системе 1, 2, 3; б) эпюр в системе трёх плоскостей проекций.
| а) | 
| б) | 
|
|
Рис. 27. Фронтально-проецирующая плоскость: а) аксонометрическое изображение, б) эпюр | |||
Угол α это угол между плоскостью γ и горизонтальной плоскостью проекций. Если во фронтально-проецирующей плоскости расположена точка, то её фронтальная проекция должна быть на фронтальном следе плоскости ( (∙) В" Є f0γ).
Профильно-проецирующая плоскость– это плоскость, перпендикулярная профильной плоскости проекций.
Пример такой плоскости приведён на рис. 28.
Если в профильно-проецирующей плоскости лежит точка, то её профильная проекция должна располагаться на профильном следе плоскости ( (∙) С''' Є р0α).
Если плоскости перпендикулярны к двум плоскостям, то также возможны три случая частных положений.
Горизонтальные плоскости– это плоскости, параллельные горизонтальной плоскости проекций 1, при этом перпендикулярные 2 и 3. Пример такой плоскости изображен на рис.29.
а) б)
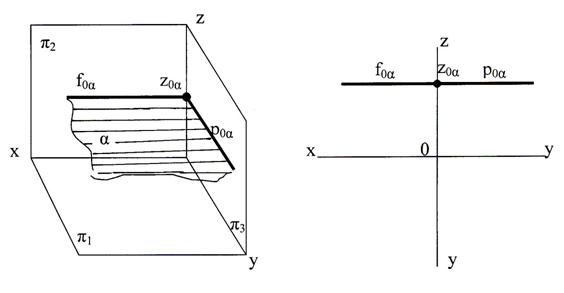
Рис.29. Горизонтальная плоскость:
а) аксонометрическое изображение, б) эпюр
Фронтальные плоскости– это плоскости, параллельные фронтальной плоскости проекций 2. При этом они перпендикулярны плоскостям 1 и 3 (рис.30).
а) б)
Рис.30. Фронтальная плоскость:
а) аксонометрическое изображение, б) эпюр
Профильные плоскости– это плоскости, параллельные профильной плоскости проекций 3. При этом они перпендикулярны плоскостям проекций 1 и 2. (рис.31).
а) б)
Рис.31. Профильная плоскость:
а) аксонометрическое изображение, б) эпюр
Дата добавления: 2018-02-28; просмотров: 1652; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!