Условие статического равновесия ЭП.
Статическая устойчивость электропривода, то есть устойчивость его в установившихся режимах работы зависит от взаимного расположения механических характеристик двигателя и рабочей машины, от величины коэффициентов жесткостиβД и βC этих характеристик.
Условием статической устойчивости электропривода является: βД-βC<0 илиβД<βC, где βД и βC – соответственно жесткости механических характеристик двигателя и исполнительного органа.
Приведите формулу механической характеристики вентилятора.
Практически механическая характестика любового производственного механизма может быть описана следующей формулой:
- начальный момент сопротивления механизма, не зависящий от скорости вращения, 
;
- номинальный момент рабочей машины, Н∙м;
α - коэффициент, характеризующий изменение момента сопротивления при изменении скорости вращения, для вентиляторов α =2.
– номинальная скорость
- скорость вращения приводного механизма, с-1;
Приведите формулу механической характеристики подъемного крана.
Practi4eski mehani4eskaya harakteristika lubogo proizvodstvennogo mehanizma mozhet bit’ opisana:
Мсо – privedennii moment pri puske;
Мсн – privedennii moment soprotivleniya pri nominal’noi nagruzke;
α – pokazatel’ stepeni;
– nominal’naya skorost’.
Для подъемных механизмов α =0; Мс = Мсн.
Приведите формулу механической характеристики металлорежущего станка.
Приведите эмпирическую формулу механической характеристики производственного механизма.
|
|
|
Различные производственные механизмы обладают механическими характеристиками, кот. можно описать следующей эмпирич-ой формулой:
Мс – момент сопр-ия производ-го механизма при угловой скорости вращения 
;
Мсо – privedennii moment pri puske;
Мсн – privedennii moment soprotivleniya pri nominal’noi nagruzke (при номинальной скорости );
α – pokazatel’ stepeni, характеризующийся изменением момента сопр-ия при изменении скорости ;
– nominal’naya skorost’.
104. Метод эквивалентного момента для выбора электрической машины по мощности, работающей в режиме S1. Ограничения.
Метод эквивалентного момента
М= СМ*I
Cправедлив для условия Ф=const и R= const . Метод не может быть применен для машин у которых Ф=var
MЭ= 
105.Метод эквивалентного тока для выбора электрической машины по мощности, работающей в режиме S1. Ограничения.
Если в распоряжении расчетчика в результате построения нагрузочной диаграммы имеются кривые тока в функции времени, то при некоторых условиях можно произвести проверку двигателя по нагреву без вычисления потерь, воспользовавшись методом эквивалентного тока.
В соответствии с (6.8) потери в двигателе можно рассматривать как сумму постоянных потерь k, не зависящих от нагрузки, и переменных I2R, всецело определяемых нагрузкой.
|
|
|
Назовем эквивалентным током такой неизменяющийся ток, при работе с которым в электрическом двигателе выделяются потери, равные средним потерям при переменном графике нагрузки, т.е.
яя мощность потерь за цикл при переменном графике нагрузки двигателя и продолжительном режиме работы
Выразив потери на каждом из участков графика D Рi через постоянную и переменную составляющие и заменив средние потери их значением через эквивалентный ток, получим:
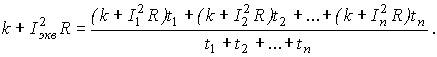Открыв скобки и сгруппировав постоянные и переменные потери, получим:
откуда эквивалентный ток при переменном графике нагрузки
или в общем случае
Вычисленный таким образом эквивалентный ток сопоставляется с номинальным током предварительно выбранного двигателя и если окажется, что Iэкв £ Iн, то двигатель удовлетворяет требованиям нагрева.
Метод эквивалентного тока, как и метод средних потерь, основан на допущении близости среднего за цикл и максимального перегревов. Это допущение не влечет за собой существенной погрешности, если выполнено условие (14). Кроме того, метод эквивалентного тока исходит из предположения независимости потерь в стали и механических от нагрузки и предполагает
|
|
|
106.Метод эквивалентной мощности для выбора электрической машины по мощности, работающей в режиме S1. Ограничения.
Метод эквивалентной мощности
P= M*ω; ω=const, Ф=const, R= const
Метод не может быть применен при ω не const
Дата добавления: 2018-02-15; просмотров: 1707; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!