Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей, когда он будет тащить первым или вторым?
Решение: предположим, что всего n экзаменационных билетов, среди которых m неизвестных. Пусть A={студент выбрал неизвестный билет, если тащит первый}, P(A)=m/n. Теперь предположим, что студент тащит билет вторым и пусть B={студент выбрал неизвестный билет, если тащит вторым}. Рассмотрим следующие гипотезы:
H1 – первый студент вытащит неизвестный билет для второго студента;
H2 – первый студент вытащит известный билет для второго студента.
События H1 и H2 образуют полную группу. P(B)=[по формуле полной вероятности]=
=P(H1)P(B\H1)+P(H2)P(B\H2)= 
.
Т.о. P(A)=P(B).
Ответ: вероятность вытащить неизвестный билет одинакова, будет ли тянуть его студент вторым или первым.
Составьте уравнение прямой, проходящей через точку А (12, 6) так, чтобы площадь треугольника, образованного ею и координатными осями, была равна 150 кв. ед.
Решение: 
a Уравнение прямой в отрезках по осям: 
A
b
В нашем случае 
; 
1) ab=300 
Уравнения 
Ответ
2) ) ab=-300 
Уравнения 
Ответ
Билет 10
Производ и диф-циалы высших порядков ф-ции многих пер-ных. Необ и достаточные условия экстремума ф-ции многих переменных.
Пусть во всех точках открытого множества 
существует частная производная 
. Эта производная как функция x может иметь в некоторой точке производную 
которая называется частной производной второго порядка и обозначается одним из символов 
Если 
, то для частной производной применяется обозначение 
Для ф-ций 2-х переменных можно записать 4-ре производные 2-го порядка в точке (x,y): 
, 
, 
, 
. Производные 
и 
называются смешанными, и они могут быть и не равны.
Теорема о смешанных производных.
Если обе смешанные производные 
и 
определены в некоторой окрестности точки 
и непрерывны в этой точке, то
= 
.
Производные порядка выше первого определяются по индукции. Например, если f(x) – функция m переменных, то 
Дифференциалы высших порядков.
Пусть функция u(x) имеет в области 
непрерывные частные производные первого и второго порядков. Тогда диффер-ал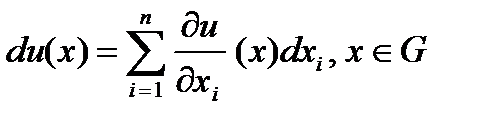 
есть функция 2n переменных, а именно 
и 
. Если фиксироывать переменные 
, то дифф-ал du(x) будет функцией x, имеющей в области G непрерывные частные производные. Тогда du(x) как ф-ция x имеет в каждой точке 
дифф-ал d(du). Если приращение независимых переменных оозначить через 
, то 
Выражение d(du(x)) есть илинейная форма относительно приращений 
. Полагая в этой билинейной форме 
, получим квадратичную форму, которая наз. вторым дифференц-ом функции u(x) в точке x и оозначается через d2u(x). Таким образом,
Аналогично полагая, что все частные производные третьего порядка непрерывны, можно вычислить первый дифференциал от d2u(x), после чего положить 
и полученную однородную форму третьего порядка назвать третьим дифференциалом функции u(x). Третий дифф-л обозначается через d3u(x). Таким образом, 
По индукции определяется дифф-л m-го порядка, в предположении, что все частные производные m-го порядка непрерывны в точке x. Если дифф-ал dm-1u(x) вычислен как однородная форма порядка m-1 относительно 
с коэфф-ми являющимися ф-циями x, то вычисляя первый диф-ал от dm-1u(x) и пологая затем, что 
при i=1,...n, получим, что dm(x) есть однородная форма порядка m, т.е.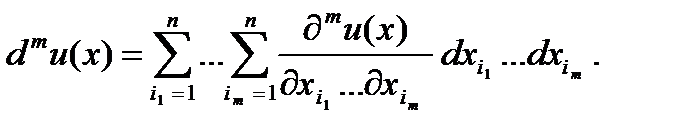 
Дата добавления: 2018-02-15; просмотров: 5599; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!