Исследовать, являются ли векторы
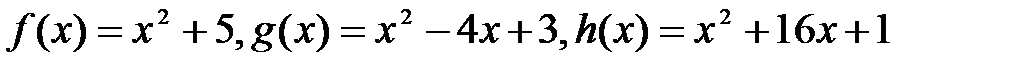
векторного пространства  линейно зависимыми.
линейно зависимыми.
Решение:
Пусть 
Это приводит к системе:


Т. к. определитель системы ≠ 0, то система имеет единственное нулевое решение. Значит, системавекторов f(x), g(x), h(x) являются линейно независимыми.
Ответ: линейно независимы.
7. Вычислите длины диагоналей параллелограмма, построенного на векторах  и
и  где
где  и
и  – единичные векторы, угол между которыми 600.
– единичные векторы, угол между которыми 600.
Решение: 

A a-b Длина
a+b
B

 Ответ:
Ответ:  .
.
Билет 8
Диф-руемость ф-ций нескольких пер-ных (частные произ-дные и диф-алы ф-ций многих пер-ных; необходимые условия диф-мости ф-ций многих переменных; достаточные условия диф-сти).
Опр: Приращением (полным) функции f в т-ке х0 наз величину

Опр1: Ф-ия f наз диффер-ой в т-ке  , если
, если  , где
, где  (*) , причем это рав-во должно выполн-я "h : x(0)+hÎU(x(0)).
(*) , причем это рав-во должно выполн-я "h : x(0)+hÎU(x(0)).
Опр2: Ф-ия f наз диффер-ой в т-ке  , если
, если 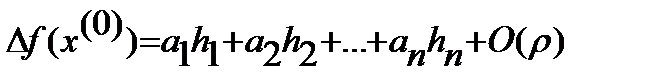 , где r=*
, где r=*
В 1 и 2 опр. O(r)=0 при r=0.
Опр3: Ф-ия f наз диффер-ой в т-ке  , если
, если
 , где ak(h)®0 при h®0, k=1,n, ak(0)=0.
, где ak(h)®0 при h®0, k=1,n, ak(0)=0.
Опр: Если $ конечн  , то его наз частной производной ф-ции f в т-ке x(0) по переем-ой x1 и обозн-ют
, то его наз частной производной ф-ции f в т-ке x(0) по переем-ой x1 и обозн-ют 
Аналог-но опред-я остальные производные по остальным переменным.
Т. (необх.усл. в т-ке) Если f диф-ма в т-ке x(0), то она в т-ке x(0) имеет все частные производные (конечные), причем  .
.
Д-во: Т.к. ф-ия f диф-ема в т-ке x(0) то 
Где  . Рассмотр вектор h=(h1,0,0,…,0)ÎRn. Тогда предыдущее выражение запишется в виде
. Рассмотр вектор h=(h1,0,0,…,0)ÎRn. Тогда предыдущее выражение запишется в виде 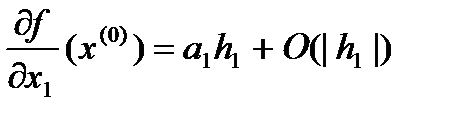 отсюда
отсюда
 . Т.о. док-ли
. Т.о. док-ли  , аналог-но док-ся другие рав-ва.
, аналог-но док-ся другие рав-ва.
|
|
|
В случае диф-ти ф-ции диф-л ф-ции запишется в виде 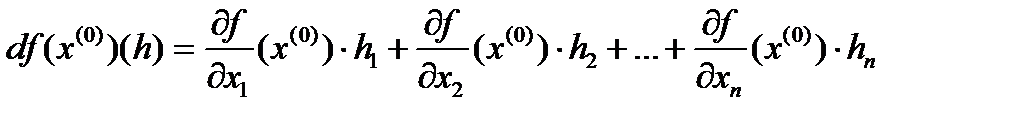 .
.
Часто вместо h1,…,hn пишут Dx1,…,Dxn, или dx1,…,dxn.


Т (дост усл диф в т-ке) пусть ф-ция u=f(x1,x2,…,xn)=f(x) имеет частные производные по всем аргументам в окрестности U(x(0)), причем эти частные производные непрерывны в т-ке x(0), тогда ф-ия f будет диф-ема в т-ке x(0).
Д-во: провед-м для ф-ции 2-х перем-ых. Рассмотр u=f(x,y) и т-ку (x0,y0), в кот-ой ф-ция u имеет произв-ые  и они непрерыв в (x0,y0). Рассмотр приращение ф-ии
и они непрерыв в (x0,y0). Рассмотр приращение ф-ии 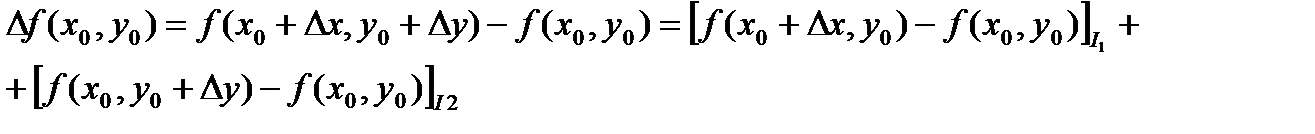
Выражение I1 можно рассмат-ть как приращение ф-ции f(x0,y0+Dy) по переем-ой x. В силу теоремы Логранжа на отрезке [x0,x0+Dx]  , 0<q1<1. Аналог-но выражение I2 можно рассматр как приращ-ие ф-ции f(x0,y0) по переем-ой y на [y0,y0+Dy] по той же теореме
, 0<q1<1. Аналог-но выражение I2 можно рассматр как приращ-ие ф-ции f(x0,y0) по переем-ой y на [y0,y0+Dy] по той же теореме  0<q2<1.
0<q2<1.
Т.к. производные непрерывны в т-ке (x0,y0), то 
Тогда аналог-но
 тогда приращение
тогда приращение
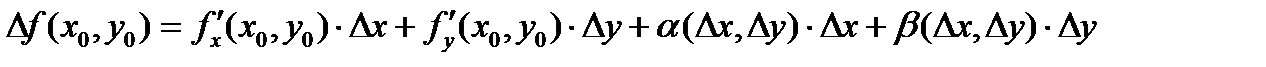 , где
, где
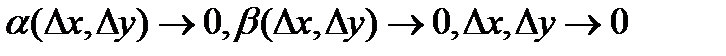 и по опр3 ф-ия f диф-ема в т-ке.
и по опр3 ф-ия f диф-ема в т-ке.
Задачи Коши. Метод характеристик. Формула Даламбера.
Задача Коши для волнового ур-я: 
Задача Коши для ур-я теплопроводности: 
Метод характеристик.
Решим задачу, описывающую колебание струны (зад. Коши для однородн. волн. ур-я): 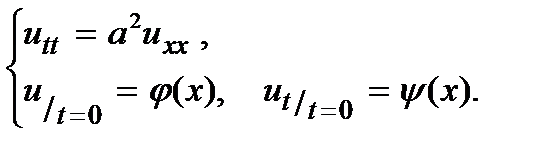 (1)
(1)
Найдём общее решение ур-я  (2), для этого приведём его к каноническому виду:
(2), для этого приведём его к каноническому виду:
Уравнение характеристик имеет вид dx=  dt (из ady=(b
dt (из ady=(b 
 )dx, где b=0, a=1, c=-a
)dx, где b=0, a=1, c=-a  , dy
, dy  dx, dx
dx, dx  dt ), характеристиками будут решения этого ур-я:
dt ), характеристиками будут решения этого ур-я:
|
|
|
x-at=c  и x+at=c
и x+at=c  .
.
Сделаем замену ξ=x-at, η=x+at, и выразив производные  и
и  через ξ и η придём к уравнению
через ξ и η придём к уравнению  =0 (канонический вид ур-я (2)).
=0 (канонический вид ур-я (2)).
Общее решение этого ур-я u=F(ξ)+Φ(η).
Сделав обратную замену получим общее решение ур-я (2): U(t,x)=F(x-at)+Ф(x+at), где F и Ф – любые дифферинц. ф-ции. Подберём эти ф-ии так чтобы выполнялись начальные условия задачи (1).

Продифференцируем первое из ур-ий, умножим на a и сложим со вторым, получим:
2aФ’(x)=ψ(x)+aφ’(x) 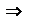 Ф’(x)=
Ф’(x)= 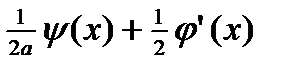 , отсюда
, отсюда
Ф(x)= 

F(x)=φ(x)-ψ(x)= 
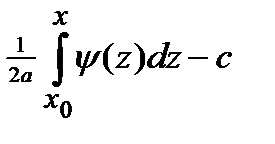 .
.
Тогда u(t,x)= 
 +
+ 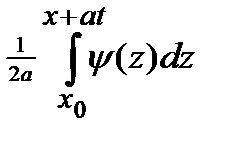 +
+
 . Сократив и преобразовав, получим решение задачи (1):
. Сократив и преобразовав, получим решение задачи (1):
u(t,x)= 
 - формула Даламбера
- формула Даламбера
8.Найти собственные значения и собственные векторы линейного оператора пространства R2, заданного в некотором базисе матрицей
 .
.
Решение:

Характеристический многочлен имеет единственный корень  кратности 2.
кратности 2.
Значит,  - собственное значение линейного оператора.
- собственное значение линейного оператора.
Найдем собственный вектор, отвечающий найденному собственному значению:
Пусть х = (х1, х2)  х(А-
х(А- 
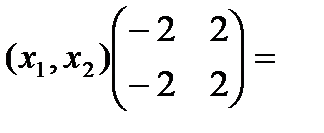 θ
θ

Пусть х2=t →x1=-t, где t – любое число
Ответ: собственное значение λ = -1, собственный вектор (-t, t), t – любое число.
8.Вычислите площадь параллелограмма, диагонали которого определяют векторы  и
и  , если
, если 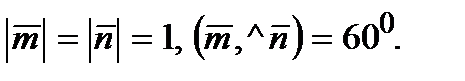
|
|
|
Решение: Воспользуемся свойством параллелограмма площадь параллелограмма, построенного на диагоналях, оказывается в 2 раза больше площади исходного параллелограмма, т.е.
q
p


 Ответ:
Ответ: 
Билет 9
Дата добавления: 2018-02-15; просмотров: 564; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
