Решить систему линейных алгебраических уравнений методом Гаусса
.Решение:Выпишем расширенную матрицу системы 
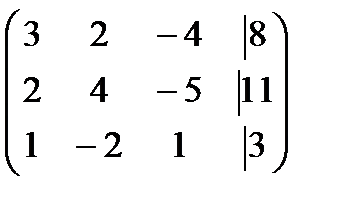
Приведем эту матрицу к ступенчатому виду. Для этого мы можем делать элементарные преобразования строк.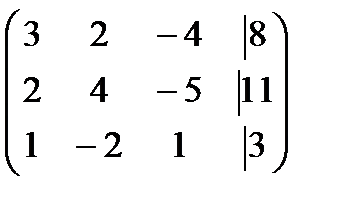 
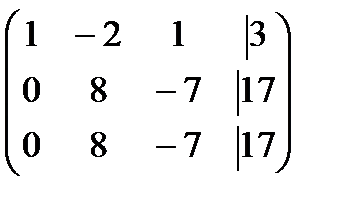
Т-ма Кронекери-Копелли: СЛУ совместима 
, когда ранг матрицы = рангу расширенной матрицы системы.
Ранг матрицы – число ненулевых строк в ступенчатом виде матрицы С – расширенная матрица системы, А – матрица системыr(C)=2r(A)=2 
r(C)=r(A) и по теореме Кронекери-Копелли система совместима. От ступенчатой матрицы переходим к ступенчатой системе: 
Т. к. число уравнений системы < числа неизвестных, то в этом случае система имеет бесконечно много решений. Чтобы найти решение, надо разбить неизвестные на главные и свободные.
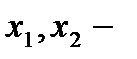главные неизвестные, 
свободная неизвестная (может быть любым числом),
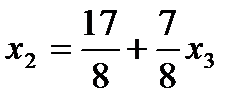
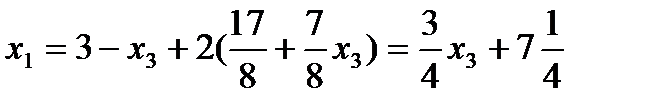
3. 
Ответ: 0.
Билет 4
Произ-ная фу-ции в точке. Дифференциал. Производные и диф-циалы высших порядков.
Опр. Пусть f определена в некоторой окрестности точки x0 ,если 
, то он называется производной функции f в точке x0(при x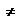 
x0) и обозначается 
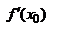. Обозначим 
∆x=x-x0, тогда 
, обозначим 
, тогда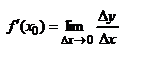 
.
Опр. Пусть f определена в некоторой окрестности U(x0), функция f называется дифференцируемой в точке x0, если 
имеет место представление 
, где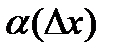 
-б.м. при 
;
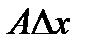наз дифференциалом функции f в т. x0 и обозначается df(x0)=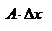 
.
Опр. Разность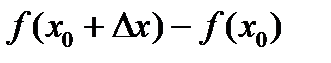 
наз приращением ф-ции в т. x0, и обозн 
. Разность 
наз приращением аргумента
Т. Если ф-ция f диф в т. x0 , то она непр в этой точке.
|
|
|
Опр. Пусть f диф-ма в некот окрестности т. x0 , т.е.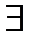 
и конечная 
, где 
. Если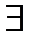 
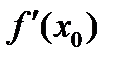то её наз второй производной f (x0) и обозначается 
.Т.о.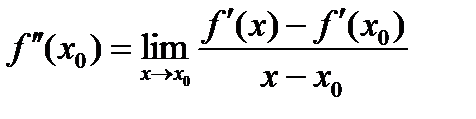 
Опр. Производная (n)-го порядка в точке x0 получается из производной в этой точке от производной (n-1) порядка. Обозначение f(0)=f. Опр. Функция f называется n раз непрерывно дифференцируемой на некотором промежутке, если у нее имеется до n-го порядка включительно и они непрерывны.
Теорема. (О вычислении производной высшего порядка)
Пусть U(x) и V(x) имеют в точке x0 производные до n-го порядка включительно, тогда их сумма и произведение имеют в точке x0 производную n-го порядка, при этом (u+v){n}=u{n}+v{n}, (uv){n}=(u+v){n}, где {n} означает, что u+v нужно формаль-но возвести в n-ю степень, а затем везде заменить степень на производную.
Вторым дифференцалом функции f в точке x0 называется дифференциал от ее первого дифференциала, предположим что 
(или dx) фиксируются. Обозначения d2y, d2f, d2f(x0), d2f=d(df)=d( dx)=d( )dx= 
dxdx= (dx)2. dnf(x0)=f(n)(x0)dxn. Свойства дифференциалов высших порядков dn(u+v)=d{n}u+d{n}v, dncu=cdnu, dn(uv)=(u+v){n}(dx)n.
Фундаментальная сис-ма решений линейного одно-ного диф-ного уравнения и его общее решение Фундаментальная сис-ма решений линейной одно-дной системы и общее решение этой системы.
|
|
|
Рассм.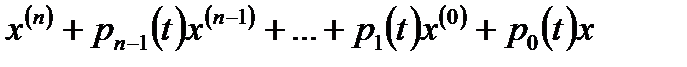 
(1)его коэффиц. непрер. на интервале 
. п-решений 
ур-ия (1) образуют фундаментальную с-му решений, если 
для кот. вроксиан 
По ф-ле Остроградского-Лиувилля 
значит если 
Значит решения 
образуют фундаментальную с-му решений на I, если вроксиан этих решений не обращается в нуль ни в одной точке из I.
Т. У всякого ур-ия (1) с непр. на I коэффиц.существует фундаментальная система ур-ий.
Д-ВО: Возьмем какое-нибудь 
и зафиксируем его. Для этого ур-ия есть только одно решение 
удовл. начальным усл-ям: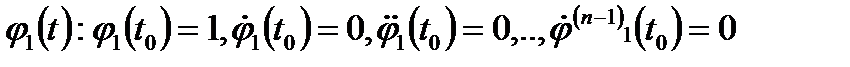 
Так же для ур-ия (1) существует единствен. решение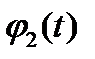 
удовлетв. нач. усл 
. то же и для решения 
Продолжая такие рассуждения докажем, что 
Вычислим вроксиан этих решений в точке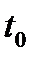 
: 
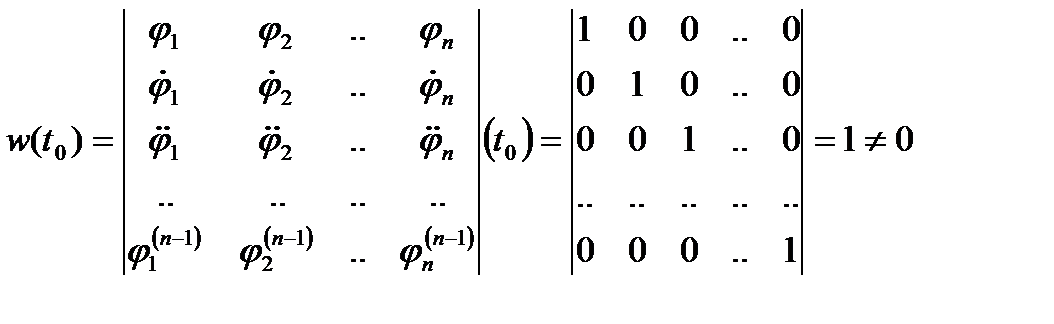
общее решение
, 
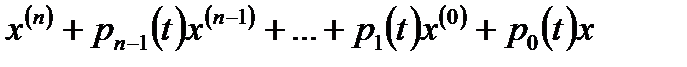коэффиц этого ур-ия непрер. на
Т. Пусть 
два решения (1), тогда 
с-const, также явл. решением ур-ия (1)
Т. Пусть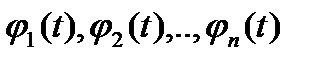 
фундаментальная система решений ур-ия (1), тогда общее решение этого ур-ия 
Дата добавления: 2018-02-15; просмотров: 778; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!