Числовые ряды (сх-ть числовых рядов; сх-сть рядов с неотр-ными членами, признаки их сх-ти; абс-тно сход-ся ряды, их св-ва; условно сх-ся ряды).

Числа натуральные, рациональные и действительные. Полнота множества действительных чисел. N назыв наименьшее из подмножеств R котор содержат 1 и вместе с каждым элементом содержат элемент на единицу больший т .е. "nnÎNÞn+1ÎN.(используются для нумерации элементов множества) Множество всех натуральных, им противоположных и нуль назыв Z. Q- назыв мн-во всех чисел вида p/q где p .  2 мн-ва назыв эквивалентными если их можно поставить во взаимнооднозначное соответствие.  Мн-во назыв счетным если оно эквивалентно N Т: R несчетно(т.к. оно имееют мощность континуума ) Док-во: докажем что даже мн-во всех R чисел (0;1) несчетно. Допустим что все эти числа перенумерованные 0; а1;а1- цифра ¹1й цифре после запятой у 1го из R чисел ; 0;а1;а2- цифра не равная 2й цифре после запятой у 2го из дейст-х чисел и так далее ; 0,a1a2a3……. Мн-во R наз полным упорядочным полем, если для него выполняются след аксиомы: 1) Определена операция слож,т.е. 2 эл ставит в соотв 3 эл , причём должны выполнятся аксиомы сложения:а)  б)   в)  г) 2) Операция умнож а)  б)  в)  г) 3) 4) Поле  наз упоряд, если его эл определено одно из соотнош удовлетворяющее cв-вом: а) справедливо одно из след утвержд б)Если , то  в) Если , то  г) Если , то         д) Если , то 5) Полным упорядоч полем наз упоряд поле , если из того что не пустых Опр: посл-ть фунд-на если "e>0$N"n>=N"m>=N|xn-xm|<e (всякая сх-ся фундаментальна) (посл-ть назыв сх-ся если $aÎR"e>0 $N"n>=N|xn-a|<e то есть а –предел посл-ти {xn} Т(о полноте д-х чисел): всякая фундаментальная последовательность д-х чисел сходится Док-во: 3 этапа:1) докажем что всякая фунд-ная ограничена;2) тогда у нее есть сх-ся. Подпослед-ть ( если хн-послед-ть и нк-строго возр-щая пос-ть натур-х чисел ; тогда. Новая посл-ть хн1 хн2 …xнк….-подпослед-ть исход послед-ти);3)докажем что вся посл-ть. Сходится к а (используя фундаментальность). Итак: (1) пусть e=1 ; найдем номер из опр-я фундаментальности ; выберем м0>=N тогда. Для любого n>N|xn-xm0|<1; пусть А=min(x1,x2,…,xN,xm0-1) тогда B=max(x1,x2,…,xN,xm0+1)тогда А<=xn<=B.(2): xnk®a(3): рассмотрим любое е>0 , e/2;найдем номер из опр-я фундам-ти для е/2 выберем подпосл-ть так чтобы некот ее элемент нк>=N ; ½xnk-a|<e/2. {xnk}подпслед-ть значит {n }строго возрастающая натур. Значит nk→∞ значит nk>=N ; тогда для любого n>=N имеем │xnk-xn│<e/2 и │ xnk-a│<e/2. Значит │xn-a│=│(xn-xnk)+(xnk-a)│<=│xn-xnk│+│xnk-a│<e/2+e/2<e. ---

Понятие диффер-ного урав-ния и его решения. Инте-мые типы ура-ний (уравнения с разд-мися переменными; линейные диф-льные уравнения, диф-ные у-ния Бернулли).

ОДУ порядка n называется соотношение вида F(x,y,y^/,...,y⁽ⁿ⁾)=0 (1). y⁽ⁿ⁾=f(x,y,y^/,...y^(n-1))- уравнение в нормальной форме. Решением ОДУ называется функция, заданная на связном множестве, дифференцируемая там n-раз и обращающая уравнение (1) на этом мн-ве в тождество.

Ф-ция j(x,C₁,C₂,...,C_n), C₁,C₂,...,C_nÎD называется общим решением уравнения (1) если:

1) для каждого набора C₁,C₂,...,C_nÎD функция одной переменной х является решением уравнения (1), j: x®j(x,C₁,C₂,...,C_n);

2) для каждого решения у(х) ур-я (1) существует набор C₁,C₂,...,C_nÎD, при котором у(х) совпадает с j(x,C₁,C₂,...,C_n).

dy/dx=f(x)g(x)-уравнение с разделяющимися переменными.

1) пусть а-корень уравнения g(y)=0, т.е. g(a)=0,тогда у=а-решение.

2) Пусть у(х), хÎ(a,b) есть такое решение, для которого g(y(х))¹0, хÎ(a,b), тогда для всякого решения должно выполнятся тождество dy(x)/g(y(x))=f(x)dx

Проинтегрируя кот., получим G(y)=F(x)+C, где C=G(y(x₀))+F(x₀)

3) помимо найденных решений м.б. решения склеенные. Это значит такие, для которых на одном участке g(y(х))¹0, а на др. g(y(х))=0. Др. Решений быть не может.

y^/=p(x)y+ q(x) –линейные ДУ.     –его решение.

y^/=p(x)y+ q(x)у^a- уравнение Бернулли. Делим обе части на у^a и заменой z= у^1-a сводим к линейному уравнению.

Решение, график которого состоит из точек единственности (т.е. если у этой точки есть окрестность, в которой графики всех решений, проходящих через эту точку, совпадают между собой) называетсячастным решением.

Решение, график которого состоит из точек ветвления (т.е., если в любой окрестности этой точки существуют решения, проходящие ч/з эту точку, графики которых в этой окрестности не совпадают между собой) называется особым решением.

---

1.

Ответ: 0.

1 плотность распределения вероятностей абсолютно непрерывной случайной величины  имеет форму Найти константу с, функцию распределения и дисперсию .

Решение:

1)

2)                 I         II

x   1 x

I)xÎ(-¥;1)

II) xÎ[1;+¥)

 

, Т.о.

3)M_x= M_x=

M_x²=

D_x= M_x²-( M_x)²=3-9/4=3/4

Ответ: с=3, D_x=3/4,

 

 

Билет 2

Послед-сти и их сход-сть (сход-еся посл-ти в топологическом прос-ве; сход-ся посл-ти дейст-ных чисел; теорема о сущес-нии предела монотонной огр-ной пос-ти; сво-ва послед-тей дейст-ных чисел, связанные с ариф-ими опе-ми над пос-тями).

Посл-тью 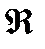 чисел наз всякое отображение мн-во  чисел во мн-во  чисел, и обозначается  (Посл-тью наз фунуция натур аргумента).

Число а наз пределом посл-ти x_n если >0 . Если послед.  имеет предел, то эту послед. наз сходящейся, в противном случаи рассходящейся_..

Посл. наз огр.,если мн-во её значений огр. Посл. будет огр., если

 Т:всякая сх-ся – ограничена

Д-во: пусть x_n→a положим =1; В=max(x ,…,x , a+1) НО обратное НЕВЕРНО.

Посл-ть- возраст-щая (убывающая), если . Возр. и убыв. послед. наз монотонными.

Т: всякая огр. посл-ть сх-ся:1) если посл-ть  возр и огр. сверху, то 2) если посл-ть  убыв и огр. снизу, то .

Д-во: пусть посл-ть возрастает и огран, это означает что , т.к. мн-во значений -огр,то это мн-во имеет sup . Пусть а=sup {x_n},докажем что ; рассмотрим >0 , поэтому имеем что , это означает что ЧТД.

Т(о связи предельного перехода с арифм операциями в множ-ве посл-тей):Если {x_n},{y_n}сх-ся посл-ти , то их сумма, произ-е,разность и частное явл. сх-ся посл-тями(в случае частного ,при допол предположении что предел Y_nне =0) .При этом lim(xn+yn)=limxn+limyn, lim(xn*yn)=limxn*limyn , lim(xn/yn)=limxn/limyn

Д-во(+): пусть xn→a, yn→b. Обозначим xn-a =pn, yn-b=qn тогда посл-ть рn ,qn б.м. (по лемме).Имеем xn+yn = a+pn+b+qn = (a+b) *(pn+qn); рn+qn б.м.(xn+yn)-(a+b) =p+qб.м., тогда посл-ть имеет предел а+b (для -,* аналогично). Для частного: xn→a ,yn→b ,b 0,док-ть что xn/yn→a/b.так как limyn =b 0 , то все эл-ты посл-ти yn начин с некоторого номера будут  0.И будем рассматривать частное xn/yn только начиная с этого номера .рассмотрим

 Это означает, что

 

2Основные теоремы теории диф-ных уравнений: теорема сущ-ния и ед-ности решения задачи Коши и методы ее док-тва; теоремы о характере зави-сти решения от параметров и начальных данных (Теорема о сущ. и ед-ти для ур-й: Пусть f и df/dy – непрерывны в обл. D, тогда какова бы ни была т. (х₀, у₀) из D у уравнения (1), $ и при том ед. реш-е у(х), удов-щее условию у(х₀)=у₀. Это решение определено по крайней мере на [x₀-h,x₀+h].

Рассм. систему ДУ

dx₁/dt=f₁(t,x₁,...,x_n)

...............................   .

dx_n/dt=f_n(t,x₁,...,x_n)          

Решением этой системы называется совокупность из n ф-ций (х₁(t),...,x_n(t)) заданных на связном множестве, диф-ых на этом мн-ве и обращающих каждое из ур-й системы в тождество.

Теорема о сущ. и ед-ти для систем: Пусть f(t,x) bdf/dx(t,x) непрерывны в некоторой области DÌRⁿ⁺¹. Тогда какова бы ни была точка (t₀,x₀)ÎD$ и при том ед. реш-е системы, уд-щее нач. условию: x₁(t₀)=x₁₀, ..., x_n(t₀)=x_n0. Это реш-е $ на некотором достаточно малом интервале [t₀-h,t₀+h].

Зав-ть реш-й от параметров. Рассм. ур-е dx/dt =f(t,x,l), (t,x)ÎD, l-пар-тр, не зав от t и х.

Т1.: Пусть ф-ция f(t,x,l) и df/dx непрерывна, как ф-ция от всех своих переменных, (t,x)ÎD, lÎ(a,b). Тогда ф-ция x(t,l) непрерывно зависит от l, т.е. , если ри некотором l₀ реш-е $ при tÎ[m,n], то "e>0 $d>0: |x(t,l)-x(t_0,,l₀)|<e при всех tÎ[m,n] и всех |l-l₀|<d. При этом реш-е x(t,l) $ при всех tÎR.

Т.2:Если f(t,x,l) и df/dx и df/dl$ и непрер. по всем (t,x,l), то х(t,l) непр и диф-ма по l.

Т.3: Если ф-ция f(t,x,l), df/dx, df/dl,d²f/dx², d²f/dxdl,d²f/dl²-$ и непрер как ф-ция своих переменных (t,x,l), то х(t,l) дважды диф-ма по l.

Т.4:Если ф-ция f(t,x,l) бесконечное число раз диф-ма как ф-ция всех своих переменных,

то х(t,l) так же диф-ма бесконечное число раз по t и по l.

Зав-ть реш-й от нач. данных. Рассмотрим ур-е dx/dt =f(t,x,l) (1). Зад. Коши –х(t₀)=x₀.

Т.: Пусть f(t,x) и df/dx непрер ф-ции, тогда j(t,t₀,x₀) есть непрер ф-ция переменных t₀,x_0.

Д-во: сделаем в ур-нии замену t=t-t₀, y=x-x₀, тогда t=t+t₀, x=y+x₀, dt=dt, dx=dy. Получаем

dy/dt=f(t+t₀,y+x₀) (2). Решение (1)- j(t,t₀,x₀) при этом перейдет в реш-е y=j(t+t₀,t₀,x₀)-x₀

ур-я (2), при чем y(0)=0, т.е. нач.данные у этого реш.фиксир.,а t₀ и x₀

входят как параметры ур.(2).

Эти параметры входят так, что для ур.(2) вып.усл.теор.о непр.зав-ти . Значит, j(t-t₀,t₀,x₀) Þj-непр.зав-ть. Если потребовать от ф-и f, чтобы она была n раз непр.-диф., то реш.j(t,t₀,x₀) будет n раздиф. По всем своим перем., в том числе и по t_0,x₀.

 

3. Найти точки разрыва функции f и установить их род и указать скачки в точках разрыва 1 рода, если f(x) = sgn(cosx).

 

- точка разрыва 1 рода, т.к.

скачок .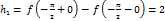

В силу периодичности все точки  – точки разрыва 1 рода и скачок в них равен 2.

Аналогично  - точка разрыва 1 рода h₂ = -2. - точки разрыва 1 рода и скачок в них равен -2.

 

2. Исследовать систему на совместимость и решить методом Крамера.

Решение:

Т-ма Крамера: крамеровская система имеет единственное решение.

Крамеровская система – это система, удовлетворяющая следующим 2-м условиям:

1) число уравнений системы = числу неизвестных

2) определитель, составленный из коэффициентов при неизвестных, отличен от 0

Составим определитель:

Система совместима, т.е. имеет хотя бы одно решение.

Ответ: (-4; 1; -2)

 

 

Билет 3

 

Числовые ряды (сх-ть числовых рядов; сх-сть рядов с неотр-ными членами, признаки их сх-ти; абс-тно сход-ся ряды, их св-ва; условно сх-ся ряды).

Пусть – числ. посл-ть, соединяя все члены это посл-ти «+»,получ. выражение кот. наз числ. рядом с членами . наз n-ой частичной суммой.

Ряд наз сх-ся, если посл-ть частичных сумм {S_n} имеет конечный предел (число). Иначе ряд наз расх-ся.

Если ряд сх-ся, то S = наз суммой ряда и пишут  . Т(критерий Коши сх-ти ряда): сходится Û"e> 0, $N : "n³N и "pÎNÞ | | <e.

Док-во: , ,пусть получ  , Cледствие 1: сх-ся когда сх-ся его остаток .Cледствие 2:Если ряд сх-ся, то необх. чтобы . Числ. ряд наз полож,если все его члены не отрицат ( ) 

Т(критерий сходимости рядов с неотрицательными членами):Пусть а_n ³ 0. "n Î N Þ сходится Û {S_n} ограничена сверху.Док-во:S_n = S_n-1 + a_n³S_n-1, "n

Необ-ть: Пусть ряд сходится Þ$lim_n®¥S_n= SÞ {S_n}- ограгичена cверху.

Дос-ть: Пусть {S_n}- неубывающая и ограгичена cверху Þ по теореме Веерштрасса $ lim_n®¥S_n = S, т.е. ряд сходится. Т(Признак Коши)Пусть полож ряд и пусть , тогда: 1)если , то исходный ряд сх-ся 2)если , то исх ряд рассх 3)если , то как сх-ть так и расх-ть ряда

Т(Признак Даламбера)Пусть задан строгополож ряд и , тогда: 1)если , то ряд сх-ся 2)если , то ряд рассх 3)если , то как сх-ть так и расх-ть ряда

Опр.Ряд наз абс сх-ся, если сх-ся ряд .

Т. Если ряд сх-ся абсолютно, то он сх-ся.

Опр.Ряд который сх-ся, но не сх-ся абс наз условно сх-ся. Т. Абс сх-ть ряда эквивалентна сх-ти двух полож рядов  и (*)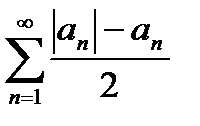

Т.Если ряд  сх-ся условно, то ряды (*) расс-ся, т.е. ряд составленный из полож членов bcc[ ряда будет рассх так же как и ряд составлен. Из отрицат членов и сх-ся ряда

Принцип суперпозиции для линейных ув-ий и систем Метод Лагранжа для ур-ний и систем (излагается сущность метода, приводится док-во соотв-щей теоремы для ур-ия или сис-мы (по выбору)).

Рассм сист . Теор: Общ реш сист предст соб сумму общ реш  соотв-ей сис-мы  и как-ниб реш самой сист . Т.о. общ реш сист  зад форм .Теор: Пусть х₁(t) – реш сист , х₂(t) –реш сист , тогда -реш сист .

Мет Лагр: Рассм Ур-е вида (1) и рассм соотв ему однор ур-е (2). Пусть -фундам сист реш д.у.(2), тогда общ реш (1) им вид: , где (t) –част реш д.у.(1).

Теор: Пусть функ 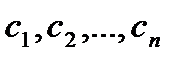удовл след сист Лагр  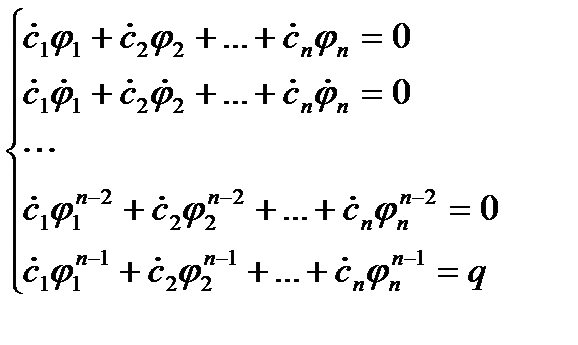тогда будет реш д.у.(1).

---

Дата добавления: 2018-02-15; просмотров: 1248; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!