Моделирование тенденции временного ряда
Для выявления основной тенденции (тренда) в уровнях ряда используется аналитический метод выравнивания. Этот способ называют аналитическим выравниванием временного ряда. Данный метод заключается в построении уравнения регрессии, характеризующего зависимость уровней ряда от временной переменной Т(t) = f(t).
Поскольку зависимость от времени может принимать разные формы, для ее формирования можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:
· линейный тренд:  ;
;
· гипербола: 
· экспоненциальный тренд:  ;
;
· тренд в форме степенной функции 
· парабола второго и более высоких порядков

Параметры каждого из перечисленных выше трендов определяют обычным МНК, используя в качестве независимой переменной время t = 1,2,…,n, а в качестве зависимой переменной – фактические уровни временного ряда Уt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
В ППП MS Exsel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1) выделите область построения диаграммы или графика; в главном меню выберите Диаграмма/Добавить линию тренда;
2) в появившемся диалоговом окне (рис.3.1) выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимации полинома.
В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение коэффициента множественной детерминации, установив соответствующие флажки на закладке Параметры (рис. 3.2);
3) щелкните по кнопке ОК.
 |
Рис 3.1. Диалоговое окно типов линий тренда
 |
Рис. 3.2. Диалоговое окно параметров линии тренда
На рис. 3.3 представлен линейный тренд, описывающий изменение объема выпуска продукции по месяцам (рассмотренный выше пример).
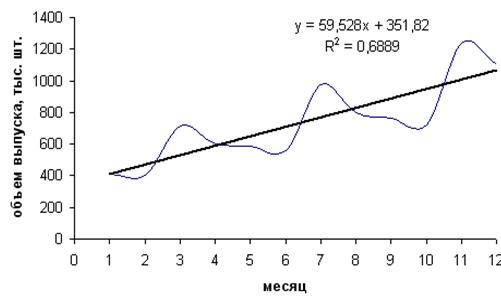
Рис. 3.3. Линейный тренд
Величина коэффициента детерминации R2 = 0,6889 позволяет сказать, что 68,89% вариации объема выпуска продукции зависит от времени, прочие факторы составляют 31,11% от общей вариации.
Моделирование сезонных и циклических колебаний
Существует несколько подходов при моделировании сезонных или циклических колебаний:
· расчет значений сезонной компоненты и построение аддитивной или мультипликативной модели временного ряда;
· применение сезонных фиктивных переменных;
· использование рядов Фурье и др.
Наиболее простым является первый метод.
Процесс построения аддитивной и мультипликативной моделей сводится к расчету значений T, S и Е для каждого порядка.
Процесс построения модели включает следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (Т+Е) в аддитивной или (Т*Е) в мультипликативной модели.
4. Аналитическое выравнивание уровней (Т+Е) или (Т*Е) и расчет значений Т с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (Т+ S ) или (Т* S).
6. Расчет абсолютных и/или относительных ошибок.
Дата добавления: 2018-02-15; просмотров: 677; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
