Наибольшее и наименьшее значение функции на отрезке.
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.
Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
1Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
2Вычислить значения функции на концах отрезка при x = a, x = b.
3Из всех полученных значений выбрать наибольшее и наименьшее.
Понятие первообразной функции.
Первообра?зной[1]или примити?вной функцией(иногда называют также антипроизводной) данной функцииfназывают такую F, производнаякоторой (на всей области определения) равна f, то есть F'= f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Неопределенный интеграл и его свойства. Геометрический смысл неопределенного интеграла.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
|
|
|
· 
· 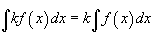
· 
· 
Множество всех первообразных некоторой функции f(x)называется неопределенным интеграломфункцииf(x)и обозначается как

Пусть задан неопределённый интеграл F(х) + С для функции f(х) в некотором интервале. При фиксированном значении С = С1получим конкретную функцию у1= F(х) + С1, для которой можно построить график; его называют интегральной кривой. Изменив значение С и положив С = С2, получим другую первообразную функцию С соответствующей новой интегральной кривой.
Таблица интегралов
Таблица основных интегралов
Методы интегрирования: непосредственный, подстановки и по частям
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
|
|
|
Пусть требуется вычислить интеграл Сделаем подстановку где — функция, имеющая непрерывную производную.
Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
Интегрирование по частям — применение следующей формулы для интегрирования:
В частности, с помощью n-кратного применения этой формулы находится интеграл
где — многочлен -ой степени.
Дата добавления: 2018-02-15; просмотров: 772; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
