Математически верное определение
Плоскость, проходящая через точку 
шаровой поверхности и перпендикулярная радиусу, проведенному в точку , называется касательной плоскостью. Точка называется точкой касания.
50. Вычисление площади поверхности тел вращения.
Площадь поверхности 
и объём 
шара радиуса 
определяются формулами:
Площадь боковой поверхности
К вычислению площади боковойповерхности цилиндра
Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой 
и длиной 
, равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
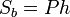
В частности, для прямого кругового цилиндра:
, и 
Площадь полной поверхности
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра: 
Площадь боковой поверхности такого конуса равна
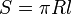
где 
— радиус основания, 
— длина образующей.
51. Вычисление объемов тел вращения. Интегральная формула для вычисления объема.
Объем кругового конуса равен
Для наклонного цилиндра существуют две формулы:
Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
|
|
|
Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):
,
где — длина образующей, а 
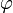— угол между образующей и плоскостью основания. Для прямого цилиндра 
.
Для кругового цилиндра:
где d — диаметр основания.
Площадь поверхности и объём шара радиуса определяются формулами:
Объем шара
Доказательство[скрыть]
Ч. т. д.
Пусть 
определена на 
. Разобьём на части с несколькими произвольными точками 
Тогда говорят, что произведено разбиение отрезка 
Далее выберем произв. точку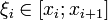 
, 
,
Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю 
, если он существует независимо от разбиения и выбора точек 
, т.е.
Если существует указанный предел, то функция называется интегрируемой на по Риману.
52. Симметрия в пространстве. Виды симметрии. Симметрия в многогранниках.
Симметрия отражения.
Если на плоскости проведена прямая mm' (рис.1) и вне ее дана точка А, то симметричной ей точкой относительно этой прямой будет точка А', лежащая на перпендикулярной mm' прямой Аа, по другую сторону от прямой на равном ей расстоянии: ВА'=BA. Прямая mm' называется осью симметрии точек А и А'. Симметрия на плоскости относительно прямой линии называется осевой симметрией, а также отражением от прямой: точка А' является как бы зеркальным отражением точки А. На рисунке справа - плоские фигуры с одной, двумя и тремя осями симметрии.
|
|
|
Аналогичной является симметрия отражения пространственной фигуры: например, если предмет состоит из двух зеркальных половин, то каждую из этих половин можно рассматривать как бы зеркальным отражением другой от воображаемой плоскости (зеркала); эта плоскость называется плоскостью симметрии. Симметрия относительно плоскости носит также название отражения в плоскости.
Центральная симметрия.
Точка A' (рис. 2) называется симметричной точке А относительно точки О, если О есть середина отрезка AA'; точка О называется центром симметрии. Два параллельных и равных между собой отрезка AB и A'B', но направленные в противоположные стороны называются обратнопараллельными. Обратная параллельность есть одно из характерных свойств фигур, обладающих центром симметрии.
Симметрия вращения.
Ось симметрии n-го порядка - линия при полном обороте вокруг которой плоская или пространственная фигура (рис. 3) несколько раз приходит в совмещение сама с собой (ось проходит через центр фигуры перпендикулярно плоскости изображения, т.е. на бумаге ось есть точка - проекция оси на плоскость - бумагу). Число совмещений при полном обороте называется порядком оси, а наименьший угол поворота, при котором фигура совмещается сама с собой, - элементарным углом поворота. На рисунке представлены изображения с осями симметрии следующих порядков: 2, 3, 4, 5, 6, 7 и соответственно элементарными углами поворота - 180, 120, 90, 72 градуса и т.д. Наряду с осью симметрииn-го порядка в каждом из приведенных изображений имеется несколько пересекающихся осей симметрии. Справа помещены два изображения, из которых верхнее можно рассматривать как имеющее ось симметрии 1-го порядка, нижнее - как имеющее осьсимметрии 5-го порядка и не имеющие осей симметрии.
|
|
|
Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение как твердого тела в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника. Иначе говоря, под действием преобразования симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани.
|
|
|
Существует одна симметрия, которая свойственна всем многогранникам. Речь идет о тождественном преобразовании, оставляющем любую точку в исходном положении. С менее тривиальным примером симметрии мы встречаемся в случае прямой правильной р-угольной призмы. Пусть a – прямая, соединяющая центры оснований. Поворот вокруг a на любое целое кратное угла 360/р градусов является симметрией. Пусть, далее, p – плоскость, проходящая посредине между основаниями параллельно им. Отражение относительно плоскости p(движение, переводящее любую точку A в точку B, такую, что p пересекает отрезок AB под прямым углом и делит его пополам) – еще одна симметрия. Комбинируя отражение относительно плоскости p споворотом 
Дата добавления: 2018-02-15; просмотров: 529; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!