Признак перпендикулярности двух плоскостей.

рис. 47	Если одна из двух плоскостей ( ) проходит через прямую (а), перпендикулярную другой плоскости ( ), то такие плоскости перпендикулярны.
рис. 48	Прямоугольный параллелепипед. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основаниям, а основания представляют собой прямоугольники.

Свойства.

В прямоугольном параллелепипеде все шесть граней представляют собой прямоугольники.

Все двугранные углы прямоугольного параллелепипеда являются прямыми

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Двугранный угол является пространственным аналогом угла на плоскости. Напомним, что углом на плоскости называется фигура, образованная двумя лучами этой плоскости с общей вершиной и частью плоскости, ограниченной этими лучами. Будем считать аналогом точки на плоскости прямую в пространстве и аналогом луча на плоскости полуплоскость в пространстве. Тогда, по этой аналогии, двугранным углом в пространстве называют фигуру (рис. 1), образованную двумя полуплоскостями, с общей ограничивающей их прямой, и частью пространства, ограниченной этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла.

Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).

Величиной двугранного угла называется величина его линейного уг­ла.

В школьном курсе геометрии доказывается, что величина линейного угла не зависит от выбора плоскости, перпендикулярной его ребру.

Найдем двугранные углы правильных многогранников.

Ясно, что двугранные углы j_куб куба (рис. 3) равны 90°_. Рассмотрим правильный тетраэдр ABCD с ребром 1 (рис. 4). Из вершин A и D опустим перпендикуляры AE и DE на ребро BC. Для нахождения двугранного угла j_тет= РAED воспользуемся теоремой косинусов, примененной к треугольнику ADE, в котором AD = 1, AE = DE = . Имеем равенство 1 = + - 2 cosj_тет. Откуда cosj_тет = , j_тет »70°30'.

Вычислим косинус двугранного угла октаэдра с ребром 1. Для этого из вершин E и F (рис. 5) опустим перпендикуляры EG и FG на ребро BC. EG = FG = . Четырехугольник AECF – квадрат со стороной 1 и, следовательно, EF = . По теореме косинусов имеем 2 = + - 2 cosj_окт. Откуда cos j_окт = - , j_окт»109°30'.

Заметим, что двугранные углы тетраэдра и октаэдра в сумме составляют 180°. Этот факт можно вывести и не вычисляя двугранных углов, а используя то, что середины ребер правильного тетраэдра являются вершинами октаэдра (рис. 6).

Вычислим косинус двугранного угла икосаэдра с ребром 1. Для этого из A и C опустим перпендикуляры AGи CG на ребро BF (рис. 7). AG = CG = . AC является диагональю правильного пятиугольника ABCDE с ребром 1 и, следовательно, AC = . По теореме косинусов, имеем = + - 2 cosj_ико. Откуда cosj_ико = - 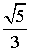, j_ико »138°11'.

Вычислим косинус двугранного угла додекаэдра с ребром 1. Для этого из вершин A и C опустим перпендикуляры AG и CG на ребро BF (рис. 8). AG = CG = AC является диагональю правильного пятиугольника ABCDE с ребром . Поэтому, AC = = . По теореме косинусов, имеем = + -2 cosj_дод. Откуда cosj_дод = - , j_дод »116°34'.

Из приведенных вычислений, в частности следует, что из равных правильных многогранников, отличных от куба, нельзя составить пространственный паркет (заполнить все пространство). Действительно, если бы, такое заполнение пространства существовало, то сумма двугранных углов правильных многогранников с общим ребром должна была быть равна 360°. Следовательно, величина двугранного угла правильного многогранника могла бы быть получена делением 360° на натуральное число. Непосредственно видно, что из правильных многогранников этим свойством обладает только куб.

Пространственный паркет можно составить используя тетраэдр и октаэдр. Для этого сначала нужно к двум противоположным граням октаэдра приставить тетраэдры (рис. 9). В результате получим параллелепипед, гранями которого являются ромбы. А уже затем из этих параллелепипедов составить пространственный паркет.

Понятие о многогранниках: параллелепипед, призма, пирамида (усеченная пирамида).

Параллелепи?пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм

Призма —многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники а боковые грани — параллелограммы

Пирами?да —многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.Пирамида является частным случаем конуса

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

 

47. Вычисление площади поверхности многогранников

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен 12. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб :-)

Иногда в задаче В9 или В11 надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхностиувеличится в девять раз, а объём — в 27 раз.

 

Понятие о телах вращения: цилиндр, конус (усеченный конус), шар.

Цили?ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченноецилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Другие виды цилиндра — эллиптический, гиперболический, параболический. Согласно определению, призма также является разновидностью цилиндра.

 Ко?нус (от др.-греч. κώνος «шишка») — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называютопирающимся на данное основание). Также можно сказать, что это тело, полученное при вращении прямоугольного треугольника вокруг одного из его катетов. Далее будет рассматриваться именно этот случай, если не оговорено обратное. Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой.

Уравнение сферы. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере.

где — координаты центра сферы, — её радиус.

Параметрическое уравнение сферы с центром в точке :

где и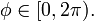

 

Если расстояние от центра сферы до плоскости больше радиуса этой сферы, то сфера и плоскость не имеют общих точек.

Если расстояние от центра сферы до плоскости меньше радиуса этой сферы, то сечениесферы плоскостью есть окружность.

В этом случае плоскость называется секущей по отношению к сфере.

Сечение шара плоскостью есть круг. Радиус сечения выражается через радиус шара и расстояние от центра шара до плоскости сечения следующим образом

.

Если секущая плоскость проходит через центр шара, то и радиус сечения равен радиусу шара. Такой круг называется большим кругом шара.

Если расстояние от центра сферы до плоскости равно радиусу этой сферы, то сфера и плоскость имеют ровно одну общую точку.

В этом случае плоскость называется касательной к сфере, а их общая точка называетсяточкой касания сферы и плоскости

Объем многогранника, описанного вокруг сферы радиусом , справедливо равенство: Где — полная поверхность многогранника. Для выпуклого многогранника, все вершины которого расположены в двух параллельных плоскостях объем можно посчитать по формуле: Где — площадь грани, расположенной в одной плоскости, — площадь грани, расположенной в другой плоскости, — площадь сечения многогранника плоскостью, равноудаленной от двух данных, — расстояние между данными плоскостями.

Касательная плоскость к сфере (шару) определяется либо как плоскость, проходящая через точку на сфере перпендикулярно радиусу, проведенному в эту точку, либо какплоскость, имеющая со сферой (шаром) единственную общую точку. Равносильность этих определений доказывается примерно так же, как и равносильность двух определений касательной к окружности в планиметрии. С точки зрения высшей математики первое определение предпочтительней, так как оно допускает естественное обобщение касательной плоскости к гладким поверхностям.

---

Дата добавления: 2018-02-15; просмотров: 840; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!