Формулы и правила дифференцирования: суммы, произведения и частного.
Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы:
1)(u±v)/=u/±v/,
2)(u·v)/=u/v+v/u,
3)(vu)=v2u/v?v/u .
Производная сложной функции.
Сложная функция–это функция, аргументом которой также является функция.
С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x)как бы аргумент функции f(g(x)).
12.Уравнение касательной к графику функции.Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f'(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m.
С угловым коэффициентом к проблем нет: мы знаем, что к = f'(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) - ка.
Осталось подставить найденные значения коэффициентов кит в уравнение прямой:
Дифференциал функции. Вторая производная.
Дифференциа?л(от лат.differentia—разность, различие) — понятие математического анализа, линейная часть приращения функции.Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства: где α – бесконечно малая в окрестности функция. Для приближенного вычисления значения функции f в точке x0 + Δx эту бесконечно малую функцию можно отбросить:
|
|
|
Линейную функцию называют дифференциалом функции f в точке и обозначают df. Для функции x производная в каждой точке равна 1, то есть Поэтому пишут:
Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.Производная от производной у' функции у называется второй производной этой функции и обозначается у" или f"(х):
y" = (y')'; f"(х) = [ f(х)]'.
Признаки возрастания и убывания функции.
дна из основных задач исследования функции — это нахождение промежутков ее возрастания и убывания. Такое исследование легко провести с помощью производной. Сформулируем соответствующие утверждения.
Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I.
|
|
|
Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I.
Экстремум функции. Необходимый и достаточный признаки существования экстремума функции.
Экстре?мум(лат.extremum—крайний) в математике — максимальноеили минимальноезначение функциина заданном множестве.
Если дифференцируемая функция y=f(x) имеет в точке x= x0экстремум, то ее производная в этой точке обращается в нуль.
Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x0 функция имеет максимум. Если же при переходе через x0 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Таким образом, если
af '(x)>0 при x<x0 и f '(x)<0 при x> x0, то x0 – точка максимума;
b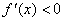 
при x<x0 и f '(x)>0 при x> x0, то x0 – точка минимума.
Дата добавления: 2018-02-15; просмотров: 994; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!