Главные площадки и главные напряжения
Выражение (2) представляет собой квадратичную форму относительно направляющих косинусов. Из линейной алгебры известно, что невырожденная квадратичная форма может быть приведена к каноническому виду, т.е. такому виду, когда члены с произведениями координат отсутствуют. Для нашего случая это будет означать, что существуют такие площадки, для которых коэффициенты при произведениях направляющих косинусов равны нулю:
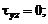
Определение.Площадки, по которым касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения, действующие по ним, — главными напряжениями.
Найдем главные напряжения. Допустим, что главная площадка существует и ее внешняя нормаль 
.
Главное напряжение по этой площадке 
Спроектируем 
на координатные оси:
Подставим это в (1) и после несложных преобразований получим
(3)
Система (3) линейна и однородна относительно направляющих косинусов. Тривиальное решение 
невозможно ввиду известного соотношения
Тогда для существования решения, отличного от тривиального, определитель системы (3) должен быть равен нулю:
Раскрывая определитель, получим кубическое уравнение относительно 
которое есть не что иное, как характеристический многочлен матрицы, составленной из компонентов тензора напряжений, а главные напряжения есть не что иное, как собственные значения этой матрицы. Характеристический многочлен выглядит так:
|
|
|
(4)
Коэффициенты уравнения (4) являются инвариантами напряженного состояния, т.е. скалярными величинами, независящими от выбора тех исходных трех взаимно перпендикулярных площадок, от которых мы отправляемся искать главные напряжения, они определяются следующим образом:
— линейный инвариант;
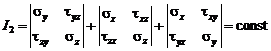
— квадратичный инвариант, равный сумме миноров элементов, стоящих на главной диагонали;
— кубический инвариант, равный определителю матрицы, составленной из компонентов тензора напряжений. Уравнение (4) имеет три действительных корня (симметричная матрица имеет только действительные собственные значения).
Корни упорядочиваются следующим образом:
где 
— наибольшее в данной точке напряжение, а 
— наименьшее.
После вычисления главных напряжений можно проверить найденные значения:
Экстремальные касательные напряжения возникают по площадкам, наклоненным к главным площадкам под углом 
Наибольшее из них равно 
(5)
|
|
|
Классификация напряженных состояний
В зависимости от числа ненулевых главных напряжений напряженные состояния классифицируются следующим образом:
1. Трехосные или объемные напряженные состояния — случай, когда ни одно из главных напряжений не равно нулю. Определение главных напряжений при трехосном напряженном состоянии подробно рассмотрено в предыдущем пункте.
2. Напряженное состояние называется двухосным или плоским, если только два главных напряжения отличны от нуля. В этом случае кубический инвариант 
равен нулю. Находим главные напряжения:
Одно из главных напряжений равно нулю, а два других определяются из решения приведенного выше квадратного уравнения. Если напряженное состояние задано напряжениями по площадкам, одна из которых, например, с внешней нормалью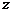 
является той главной площадкой, по которой главное напряжение равно нулю, то тензор напряжений принимает вид
Инварианты напряженного состояния примут вид
Подставляя это в выражение для главных напряжений, получим формулу
|
|
|
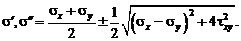(6)
Данная формула применима не только в случае плоского напряженного состояния, но и в случае трехосного напряженного состояния, когда известно положение одной из главных площадок. В этом случае по этой формуле определяются два других главных напряжения.
3. Если кубический и квадратичный 
инварианты одновременно равны нулю, то лишь одно главное напряжение отлично от нуля. Оно называется одноосным или линейным и возникает, например, при растяжении и сжатии при чистом изгибе.
Помимо приведенной выше классификации, возможна классификация, основанная на знаках главных напряжений:
1. Трехосные растяжения, когда ни одно из главных напряжений не является сжимающим.
2. Трехосные сжатия, когда ни одно из главных напряжений не является растягивающим.
3. Смешанные напряженные состояния, когда и имеют разные знаки.
Дата добавления: 2018-02-15; просмотров: 666; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!