Определение перемещений в балках.
В балках возникают два типа перемещений:
1) Линейные перемещения – прогибы, т.е. перемещение точек оси балки в направлении перпендикулярном оси.
2) Угловые перемещения – углы поворота сечений, т.е. углы, на которые поворачиваются при изгибе поперечные сечения.
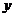- прогиб; 
- угол поворота
. Очевидно,
что 
т.к. 
, то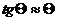 
, откуда следует связь:
Первая производная от прогиба есть угол поворота сечения 
Расчет балок на жесткость производится из условия: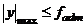 
Величина 
называется допускаемым прогибом и зависит от характера конструкции и условий ее работы.
ЭЛЕМЕНТЫ ТЕОРИИ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
Напряженное состояние в точке.
Мерой внутренних сил, величиной характеризующей интенсивность их распределения является напряжение.
Рассмотрим тело, находящееся под действием системы уравновешенных сил.
Будем исследовать внутренние силы в малой области, окружающей точку А. Проведем через данную точку сечение некоторой поверхностью. Внешняя нормаль этой поверхности в точке А -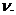 
Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки А площадку 
. Результирующая внутренних сил, действующих на площадке пусть равняется 
.
Делим результирующую силу 
на 
, получаем величину среднего напряжения по площадке 
. Величина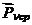 
зависит от размеров площадки, перейдем к пределу, стягивая площадку к точке
|
|
|
Величина 
- называется вектором полного напряжения в данной точке по площадке с внешней нормалью 
.
Очевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.
Совокупность всех векторов полного напряжения по площадкам, про 
ходящим через данную точку, составляет напряженное состояние в данной точке.
Если взять другим образом ориентированные площадки, то в общем случае получим другие значения вектора напряжения. И так как через данную точку можно провести бесконечное число площадок, то имеется бесконечная совокупность векторов напряжения, которая и представляет собой напряженное состояние в данной точке.
Можно вычислить напряжение по любой площадке, проходящей через точку, если известны напряжения по любым трем взаимно перпендикулярным площадкам, проходящим через эту точку. Докажем это положение.
Выделим в окрестности точки малый прямоугольный параллелепипед с гранями, параллельными координатным плоскостям.
Внешними нормалями граней параллелепипеда будут оси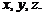 
Полное напряжение по каждой из граней можно разложить на три составляющие, направленные по координатным осям. Всего получится 9 компонент: три нормальных и шесть касательных напряжений. Нормальные напряжения будем обозначать буквой 
с индексом, соответствующим внешней нормали площадки. Например, 
означает нормальное напряжение по площадке с внешней нормалью 
Растягивающее нормальное напряжение, как обычно, считается положительным. Касательное напряжение обозначается буквой 
с двумя индексами. Первый индекс указывает нормаль площадки, по которой действует напряжение, а второй — указывает, по какой оси направлено напряжение. Например: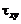 
— касательное напряжение по площадке с внешней нормалью 
параллельное оси 
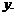Касательные напряжения считаются положительными, если при положительном направлении внешней нормали они направлены в сторону положительного направления осей. Докажем, что касательные напряжения по взаимно перпендикулярным площадкам равны. Так как тело, из которого вырезан элемент, находится в равновесии, то в равновесии должен находиться и рассматриваемый элемент. Запишем условие равенства нулю суммы моментов относительно координатных осей:
|
|
|
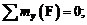
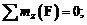
Раскроем первое из этих уравнений, приняв длины ребер параллелепипеда соответственно равными 
|
|
|
Поступая таким же образом с двумя другими уравнениями, будем иметь:
Мы получили закон парности касательных напряжений: касательные напряжения по взаимно перпендикулярным площадкам равны. Благодаря этому закону число независимых компонент напряжения уменьшается до шести.
Совокупность напряжений по трем взаимно перпендикулярным площадкам определяет тензор напряжений, симметричный по причине закона парности касательных напряжений:
Покажем, что если задан тензор напряжений, то можно определить напряжения по любой площадке, проходящей через данную точку. Выделим малый тетраэдр, содержащий данную точку, по трем граням которого заданы напряжения, т.е. задан тензор напряжений. Требуется определить напряжения по четвертой площадке, наклонной к координатным плоскостям. Внешняя нормаль наклонной площадки 
— 
Она задается направляющими косинусами:
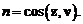
Площадь грани АВС обозначим 
Тогда площади граней, совпадающих с координатными плоскостями, выразятся так: 
— 
— 
— 
|
|
|
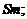
Будем искать компоненты полного напряжения 
направленные соответственно по осям 
Спроектируем все силы, действующие на элемент, на координатные оси, выразим искомые величины через компоненты тензора напряжений:
(1)
Зная компоненты, определяемые соотношениями (1), найдем полное напряжение:
Для того чтобы найти нормальное напряжение по наклонной площадке, надо спроектировать составляющие 
на направление нормали 
Подставляя сюда формулы (1), получим
(2)
Касательные напряжения можно найти по формуле
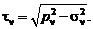
Таким образом, так как наклонная площадка совершенно произвольна, то можно утверждать, что задание тензора напряжения полностью определяет напряженное состояние в данной точке, т.е., зная компоненты тензора, можно найти полное, нормальное и касательное напряжение по любой площадке, проходящей через данную точку.
Дата добавления: 2018-02-15; просмотров: 612; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!