Влияние условий закрепления концов стержня на величину критической силы.
Формула (2) дает возможность определить критическую
силу только в случае шарнирного опирания обоих концов стержня. Обобщим полученный результат на некоторые другие часто встречающиеся случаи закрепления.
а) Стержень, закрепленный жестко одним концом и свободный от закрепления на другом.
Очевидно, изгиб стержня в этом случае будет таким же, как и в случае шарнирно опертого стержня, но имеющего длину в 2 раза большую.
Критическая сила в этом случае будет равна критической силе шарнирно опертого стержня, имеющего длину 
Введем понятие коэффициента приведения длины - 
, т.е. числа показывающего во сколько раз нужно увеличить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной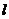 
при заданном закреплении. Очевидно, что в нашем случае 
.
Коэффициент можно трактовать как число, показывающее сколько раз длина стержня укладывается в длине полуволны синусоиды, по которой происходит потеря устойчивости.
Обобщим формулу Эйлера 
Для некоторых других случаев закрепления коэффициент приведения длины равен:
Пределы применимости формулы Эйлера.
Формула Эйлера выведена в предположении, что материал линейно упруг, и , естественно, применима в тех случаях пока справедлив закон Гука.
Придадим формуле (3) иной вид.
Введем понятие критического напряжения, т.е. напряжения соответствующего критической силе
|
|
|
но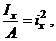 
где 
- минимальный радиус инерции сечения.
Введем еще одну величину – гибкость стержня 
тогда 
Тогда можно сказать, что формула Эйлера справедлива, если критические напряжения не превышают предела пропорциональности при
сжатии. 
Выясним, при каких гибкостях можно использовать формулу Эйлера.
Приравняем в (4) 
Если 
то можно использовать формулу (3).
Для малоуглеродистых сталей, особенно часто используемых для сжатых элементов: 
тогда
т.е. для малоуглеродистых сталей формулу Эйлера можно использовать при гибкостях больших 100.
Приведенное выше решение пригодно только для сравнительно длинных и тонких стержней. В случае более коротких и жестких стержней потеря устойчивости происходит при возникновении пластических деформаций, и задача требует специального рассмотрения. Существуют решения (Т.Карман, Энгессер) об устойчивости стержня за пределами упругости. Иногда прибегают к эмпирическим формулам типа формулы Ясинского 
где
и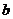 
- константы, зависящие от свойств материала.
Коэффициент запаса на устойчивость.
Представляет собой отношение критической силы для стержня к силе действующей на него 
|
|
|
Коэффициент запаса на устойчивость может выступать, как некоторая заданная нормативная величина, тогда 
где 
- нагрузка, допускаемая из условия устойчивости.
Дата добавления: 2018-02-15; просмотров: 561; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!