Деформированное состояние в точке
Деформированное состояние в точке определено, т.е. можно вычислить удлинение по любому направлению, проходящему через данную точку, если задан тензор деформаций. Тензор деформаций представляет собой совокупность удлинений по трем взаимно перпендикулярным направлениям и углов сдвига в плоскостях трех площадок, нормальных к данным направлениям. Он имеет следующий вид:
(7)
Здесь 
— деформации относительного удлинения в направлении соответствующих осей; 
— углы сдвига в соответствующих координатных плоскостях. Тензор деформаций симметричен. Теория деформированного состояния аналогична теории напряженного состояния.
Теории предельных напряженных состояний.
Материал, из которого выполнена конструкция, может находиться в различных механических состояниях. При сравнительно небольших нагрузках материал работает упруго. Его поведение может быть описано законом Гука. По мере роста нагрузок материал переходит в упругопластическую стадию, возникают значительные остаточные деформации. Происходит коренное изменение механических свойств материала. Затем появляются трещины, которые разрастаются и материал переходит в стадию разрушения, что также говорит о коренных в нем изменениях.
Механическое состояние материала в точке зависит в первую очередь от напряженного состояния в данной точке. Правда, механическое состояние зависит не только от напряжений, но и от других факторов (истории нагружения, влияния температуры и скорости нагружения), но учет влияния этих факторов чрезвычайно затруднителен, поэтому приходиться вводить допущение о том что механическое состояние в точке зависит только от напряженного состояния в данной точке.
|
|
|
Напряженное состояние, при котором происходит коренное изменение механического состояния материала в точке, называется предельным напряженным состоянием.
Как можно понять из того, что было сказано выше, имеются два различные предельные состояния:
1) Переход материала в данной точке в пластическое состояние.
2) Наступление стадии разрушения.
Для оценки наряженных состояний надо знать механические характеристики материалов, которые определяются из испытаний, проводимых над образцами. Для того чтобы результаты испытаний были достоверными, необходимо обеспечить в образце однородное, т.е. не меняющееся от точки к точке, напряженное состояние. Это возможно в полной мере при испытании образца на растяжение и отчасти при испытании короткого образца на сжатие и тонкостенной трубки на кручение.
Основным видом испытания, как мы знаем, является испытание на растяжение.
|
|
|
Таким образом, ставится следующая задача: Отправляясь от экспериментов проведенных в условиях одноосного растяжения, дать оценку напряженного состояния в конструкции.
Если конструкция работает в условиях одноосного напряженного состояния (растяжение, сжатие, чистый изгиб), то сделать это несложно. Коэффициент запаса в этом случае определяется
- коэффициент запаса по текучести
- предел текучести при растяжении
- напряжение в наиболее опасной точке конструкции.
В случае сложного напряженного состояния (двухосного, трехосного) сделать это сложнее. Прежде всего обобщим понятие коэффициента запаса на случай сложного напряженного состояния.
Под коэффициентом запаса будем понимать число, в которое надо увеличить одновременно все компоненты напряженного состояния чтобы оно стало предельным.
Различные напряженные состояния, имеющие одинаковые коэффициенты запаса, т.е. одинаково близкие к предельному напряженному состоянию, будем называть равноопасными.
Введем основное в теории предельных напряженных состояний понятие: эквивалентное напряжение – напряжение, которое надо создать в растянутом образце, чтобы его напряженное состояние было равноопасно заданному сложному напряженному состоянию. Величина эквивалентного напряжения устанавливается с помощью соответствующей теории (гипотезы) предельного напряженного состояния.
|
|
|
Величина коэффициента запаса по текучести определяется че
рез эквивалентное напряжение следующим образом: 
Обобщенный закон Гука
Между компонентами тензора деформаций (2.7) и компонентами тензора напряжений (1.5) существует связь, которая, в принципе, может быть установлена только экспериментальным путем. Опыт показывает, что для большинства материалов при умеренных нагрузках связь между напряжениями и деформациями может быть принята линейной. Это обнаруживается при испытании стандартных образцов в условиях одноосного растяжения. Вплоть до значения напряжения 
называемого пределом пропорциональности,справедлив закон Р. Гука (1676 г.): напряжения прямо пропорциональны деформации удлинения:
(2.9)
В законе Гука коэффициент пропорциональности 
называется модулем упругости.Он характеризует жесткость материала и в приведенных ниже случаях приблизительно равен: сталь — 
МПа; алюминиевые сплавы — 
МПа; древесина вдоль волокон (сосна) — 
МПа.
|
|
|
Закон Гука можно записать в виде
Воспользуемся этим соотношением и принципом независимости действия сил для того, чтобы получить закон Гука для трехосного напряженного состояния. Обратим внимание на то, что с точностью до малых высшего порядка нормальные напряжения не вызывают сдвигов, а касательные напряжения не вызывают удлинений ребер элемента. Рассмотрим малый элемент, показанный на рис. 2.3. Пусть на элемент действует только напряжение 
а 
тогда деформации в направлении координатных осей будут равны:
При 
и 
При 
и 
Деформация удлинения в направлении оси 
при совместном действии всех напряжений будет равна
Аналогичным образом определятся деформации в направлении других координатных осей. Подставляя выражения для 
после очевидных преобразований получим три уравнения:
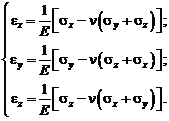(2.10)
Добавим к этим уравнениям еще три соотношения, вытекающие из закона Гука при чистом сдвиге (двухосное напряженное состояние, при котором на гранях элемента возникают только касательные напряжения):
(2.11)
Три упругие постоянные (модуль упругости 
модуль сдвига 
и коэффициент Пуассона 
) не являются независимыми. Они связаны между собой соотношением
(2.12)
Шесть полученных уравнений, связывающих между собой компоненты тензоров напряжений и деформаций, составляют так называемый обобщенный закон Гука.
Три дифференциальных уравнения равновесия, шесть соотношений Коши и шесть уравнений обобщенного закона Гука составляют систему уравнений теории упругости, в которой неизвестными будут шесть независимых компонент тензора напряжений, шесть независимых компонент тензора деформаций и три компоненты вектора перемещения.
Дата добавления: 2018-02-15; просмотров: 585; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!