Преобразователи частоты (модуляторы)
Назначение - изменение электрического представления сигналов с целью наиболее эффективного использования линий связи при передаче информации.

 |
Рис.5.2-Обозначения преобразователей частоты
Обозначения сигналов, подаваемых на модуляторы, следующие.
a(t) - модулирующий сигнал;
f(t) - модулируемый сигнал;
S(t) - модулированный сигнал.
Классификация и формы модулированных сигналов
Модулированные сигналы в зависимости от типа сигнала или несущего колебаний делятся на три класса .
1. Аналоговая модуляция.
2. Дискретная модуляция .
3. Импульсная модуляция .
В зависимости от того, какой параметр подвергают изменению при модуляции, они делятся на подклассы.
Аналоговая модуляция бывает:
- амплитудная (АМ) (рис.5.4);
- частотная (ЧМ);
- фазовая (ФМ).
Дискретная модуляция:
- дискретная аналоговая (ДАМ);
- дискретная частотная (ДЧМ);
- дискретная фазовая (ДФМ).
Для импульсной модуляции, переносчиком информации является последователь-ность импульсов со скважностью Q>>1.
Импульсная модуляция бывает следующих видов:
- амплитудно-импульсная (АИМ);
- широтно-импульсная (ШИМ), которая в свою очередь делится на: ШИМ1 и ШИМ2 (рис.5.3);
 |
Рис.5.3-Разновидности широтной модуляции ШИМ1 и ШИМ2
-фазоимпульсная (ФИМ)или времяимпульсная (ВИМ).
ШИМ1 - изменению подвергается только передний фронт (например, левый) импульса.
|
|
|
ШИМ2 - изменению подвергаются оба фронта пропорционально.
 |
Рис.5.4-Формирование АМ сигнала
 |
 , (5.3)
, (5.3)
Рис.5.5-Формирование сигналов дискретной модуляции

 |
Амплитудная модуляция
Нормируем сигнал a(t) таким образом сигнал, чтобы  .
.
В качестве цели последующего анализа поставим перед собой расчет спектра амплитудно-модулированного сигнала.
 |
Рис.5.7-Спектр сигнала a(t)
Амплитудно-модулированный сигнал можно записать в виде
 .
.
Обозначим  - спектр сигнала a(t) (рис.5.7).
- спектр сигнала a(t) (рис.5.7).
Выполняя прямое интегральное преобразование Фурье, получаем

С учётом известного выражения (формула Эйлера)

а также заменяя интегралы дельта-функцией согласно формуле
 ,
,
окончательно получаем
 |
 . (5.4)
. (5.4)
 Формирование спектра сигнала АМ в соответствии с выражение (5.4) поясняется рис.5.8.
Формирование спектра сигнала АМ в соответствии с выражение (5.4) поясняется рис.5.8.
С учётом условия физической реализуемости спектр сигнала АМ будет иметь место только в области положительной полуоси частот. На рис.5.9 представлена структура спектра АМ сигнала, состоящего из двух основных составляющих: нижней боковой полосы частот (н.б.) и верхней боковой (в.б.).
|
|
|
Способы передачи АМ сигналов
В промышленных телекоммуникационных системах (многоканальных системах передачи информации) применяются следующие способы передачи АМ сигналов [10].
1 способ. Передача 2-х боковых полос частот и несущего колебания (ДБП) (рис. 5.10 и 5.11)
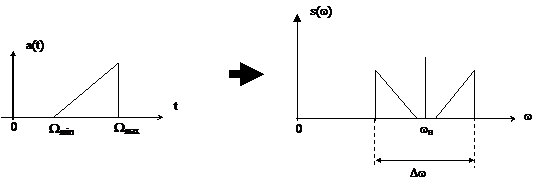 |
Рис.5.10-Спектральные диаграммы формирования
сигнала ДБП с несущим колебанием
Основное достоинство этого метода заключается в простоте построения оборудования на передаче и приёме.
Основные недостатки:- в линию передаются мощности обеих боковых и несущее колебание ;
- ширина полосы линейного спектра равна  .
.
 |
Рис.5.11-Схема формирования сигнала ДБП с несущим колебанием
 |
 |
Рис.5.12-Спектральные диаграммы
формирования сигнала ОБП
Рис.5.13-Схема формирования сигнала ОБП
2 способ. Одна боковая полоса частот (ОБП) (рис. 5.12 и 5.13).
Главное достоинство этого метода, которое обусловило его широкое применение в современных телекоммуникационных системах, заключается в том, что в линию передаётся только одна боковая полоса частот.
Недостаток – усложнение оборудования на передаче и приёме.
|
|
|
3-й способ. Одна боковая и несущая (рис. 5.14)
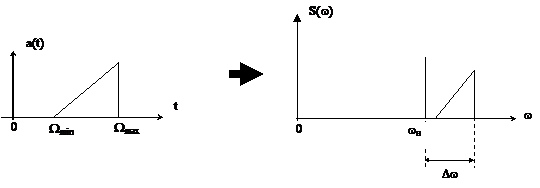 |
Рис.5.14-Спектральные диаграммы формирования
сигнала ОБП с несущим колебанием
Достоинства:
1. Полоса частот достаточно мала (  ).
).
2. Нет необходимости формировать несущее колебание на приемнике.
Недостаток - несущее колебание перегружает устройства передачи.
По сложности реализации этот способ занимает промежуточное место между 1-м и 2-м способами.
4-й способ. Частичное подавление одной боковой полосы частот (рис. 5.15).
Используется, например, в телевидении, в телефаксах. Применение связано с тем, что сигнал, передающий изображение, имеет спектральные составляющие, близкие к нулевой частоте.
Этот способ в реализации достаточно сложен.
Главное достоинство заключается в том, что этот способ позволяет передавать сигналы с частотами, близкими к нулю.
 |
Рис.5.15-Спектральные диаграммы формирования
сигнала с частичным подавлением одной
боковой полосы частот
ЛЕКЦИЯ 6
МОДУЛЯТОРЫ
Угловая модуляция. Дискретная амплитудная модуляция (ДАМ). Дискретная фазовая модуляция (ДФМ). Дискретная частотная модуляция (ДЧМ). Импульсные виды модуляции. Модуляция случайными сигналами
|
|
|
Угловая модуляция
Как правило, ФМ и ЧМ объединяются в угловую модуляцию.
Девиация частоты (Dw) - абсолютное максимальное изменение частоты.
Закон изменения частоты (рис.6.1):
 ,
,
 .
.
 |
Рис.6.1-Изменение частоты при частотной модуляции
Q(t) - мгновенный угол.
При частотной модуляции мгновенный угол (фаза) будет иметь вид

 (6.1)
(6.1)
где bчм - индекс частотной модуляции.
В этом виде модуляции индекс bчм зависит от частоты модулирующего колебания.
При фазовой модуляции
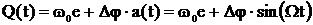 , (если
, (если 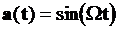 ).
).
 , (6.2)
, (6.2)
где bфм - индекс фазовой модуляции.
По сравнению с частотной модуляцией bфм не зависит от частоты модулирующего колебания.
Так как:
 ;
;
 ;
;
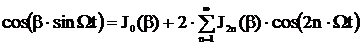 .
.
где  - функция Бесселя первого рода n-го порядка от аргумента
- функция Бесселя первого рода n-го порядка от аргумента  . После выполнения несложных преобразований, получим
. После выполнения несложных преобразований, получим
 (6.3)
(6.3)
Замечания к этому выражению.
1. Формула получена без применения прямого интегрального преобразования Фурье.
2. Спектр состоит из 3-х частей:
1-е слагаемое - несущее колебание с амплитудой, определяемой функцией Бесселя J0(b);
 |
2-е слагаемое - бесконечное количество разностных частотных продуктов;
3-е слагаемое - бесконечное количество суммарных частотных продуктов.
Даже в идеальном случае спектр бесконечен. С ростом k амплитуда быстро убывает.
Пример спектра сигнала с угловой модуляцией приведён на рис.6.2.
Рис.6.2-Спектр сигнала угловой модуляции
Оценим ширину спектра DS.
Если  :
:
- при ЧМ  (ширина спектра не зависит от
(ширина спектра не зависит от  );
);
- при ФМ  (ширина спектра зависит от частоты сигнала W).
(ширина спектра зависит от частоты сигнала W).
При  ,
,  ,
,
Дата добавления: 2018-02-15; просмотров: 1530; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
