Спектр непериодического сигнала

   Для определения спектра непериодического сигнала применяют непосредственно формулу прямого преобразования Фурье (2.9).

   Выражения (2.9) и (2.10) справедливы только для абсолютно интегрируемых сигналов s(t), для которых справедливо условие

 

                                                                                 (2.21)

 

   Это означает, что сигнал s(t) ограничен во времени, т.е. физически реализуем, с конечной энергией.

   Выражение (2.9) представляет спектр непериодического сигнала в виде бесконечной суммы (интеграла) гармонических колебаний (составляющих) с бесконечно малыми амплитудами. Из сравнения (2.9) с рядом Фурье (2.13) видно, что амплитуды этих гармонических колебаний составляют [3]

 

   .

 

   Выделив какую-либо дискретную частоту W_n = nW₁, соответствующую, в случае периодического сигнала, n-й гармонике, получим для амплитуды этой гармоники выражение

 

  

 

   В случае же непериодического сигнала, совпадающего с s(t) на интервале  получим для спектральной плотности соответствующей той же частоте W=W_n, следующее выражение:

   .

   Так как интегралы в правых частях этих выражений полностью совпадают, заключаем, что (jW_n)=T₁C_n.

   Или, учитывая, что ,

                                                                                   (2.22)

   (jW_n) получается путем деления амплитуды n^-ой гармоники   на полосу частот F₁, отделяющую соседние линии дискретного спектра (рис.2.7). Следовательно, (jW_n) имеет смысл плотности амплитуд и обладает размерностью [амплитуда/герц].

 

Спектр случайного сигнала

   С помощью прямого преобразования Фурье (2.9) определить спектр случайного сигнала в общем виде нельзя, так как интеграл от случайного сигнала на бесконечном интервале его существования расходится.

   Введём следующие ограничения [3]. Возьмем стационарный, в широком смысле, эргодический сигнал. Ограничимся k^-й реализацией такого сигнала на отрезке . Спектр (преобразование Фурье) такой финитной функции (ограниченной на интервале  и отличной от 0)  определится по формуле (2.9):

 

  

 

   Из этого выражения следует сделанный ранее вывод - при T®¥ спектр  неограничен.

   Если 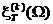 - напряжение или ток на нагрузке 1 Ом, то средняя мощность на частоте W, отнесенная к полосе , т.е. спектральная плотность мощности усеченной реализации равна:

 

   .

 

   При T®¥ случайная величина G_T(W) (на множестве реализаций) не стремится, вообще говоря, к определенному интегралу. Поэтому в качестве спектральной характеристики принимают предел при T®¥ средней величины спектральной плотности мощности усеченной реализации.

 

              .                 (2.23)

 

   Эту функцию называют спектральной плотностью средней мощности случайного сигналаx(t).

   Теоретически, в соответствии с этой формулой, можно построить электронное устройство для измерения спектра стационарного в широком смысле случайного сигнала. Однако реализация такого устройства экономически нецелесообразна ввиду значительной сложности алгоритма измерения по формуле (2.23).

   На практике, если известна нормированная автокорреляционная функция случайного сигнала B_x(t), применяют следующую формулу для оценки спектра случайного сигнала:

 

              ,                                             (1.24)

 

при условии, что B_x(t) абсолютно интегрируема, т.е. выполняется условие

 

              .                                                                    (1.25)

 

Замечание: Для того, чтобы условие (1.25) выполнялось, достаточно, чтобы сигнал x(t) был центрируем.

   Формула (1.24) означает, что спектральная плотность средней мощности сигнала получается преобразованием Фурье от автокорреляционной функции этого сигнала. Отсюда следует также, что автокорреляционная функция получается обратным преобразованием Фурье от спектральной плотности средней мощности стационарного в широком смысле случайного сигнала:

 

    .                                           (1.26)

   Формулы (1.24) и (1.26) являются аналитическим представлением теоремы Хинчина - Винера: автокорреляционная функция и спектральная плотность средней мощности стационарного в широком смысле случайного сигнала связаны между собой парой преобразования Фурье.

   Замечая, что автокорреляционная функция и спектральная плотность средней мощности являются четными функциями, можно перейти к более распространённым на практике формулам:

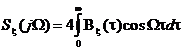              .                                                             (1.27)

              .                                                 (1.28)

   Эти формулы называют тригонометрической формой представления теоремы Хинчина - Винера.

Рассмотрим некоторые частные случаи.

Величина

              ,                                                  (1.29)

равна дисперсии (мощности) случайного сигнала.

Величина спектральной плотности средней мощности при w = 0 (1.30) равна

              .                                                       (1.30)

Под шириной спектра понимается отношение площади, ограниченной спектральной характеристикой сигнала, к спектральной плотности на какой-то конк-ретной частоте.

              .                                     (1.31)

Если , тогда

               .                                                                   (1.32)

 

Интервал корреляции определяется по формуле

              .                                             (1.33)

 

 

Учитывая (1.29) и (1.30), можно записать

        .                                                                       (1.34)

 

 

Это соотношение имеет важное значение для практики при быстрой (инженерной) оценки ширины спектра сигнала при известном интервале корреляции.

---

Дата добавления: 2018-02-15; просмотров: 1454; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!