Дискретное представление сигналов

 

   Дискретное представление аналогового сигнала s(t)ÎS(t) на интервале Т есть изображение этого сигнала в виде последовательности координат [5]

 

                                                                                    (2.35)

 

по значениям которых может быть получена оценка 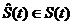 исходного аналогового сигнала.

   Дискретное представление и обратное ему преобразование - восстановление исходного сигнала в виде оценки  можно записать в общей форме:

 

              s(t);  tÎT;                                  (2.36)

 

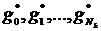              ( ); tÎT_,                                                                          (2.37)

 

где  - оператор представления;

    - оператор восстановления;

   T - интервал представления;

    - принятые приёмником системы передачи значения координат с искажением, по которым производится восстановление исходного сигнала.

   Погрешность восстановления

 

              e_å(t)= 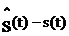                                                                  (2.38)

 

является реализацией случайной функции

       

              E_å(t)=                                                                 (2.39)

 

и характеризуется средним (по множеству и времени) квадратом  или, чаще, его приведенным (к дисперсии сигнала ) значением :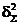

 

                                              (2.40)

 

   Фактически это суммарная погрешность (шум представления) системы передачи, в которую входят составляющие, возникающие за счет всех преобразований исходного сигнала в тракте передачи.

   Операция (2.36) выполняется на передающей стороне оборудованием преобразования сообщения в сигнал с каналом передачи, операция (2.37) – оборудова-нием преобразования принятого из канала сигнала в сообщение.

   Восстановление сигнала в аналоговой форме 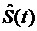 может и не делаться, поскольку часто обработка проводится на ЭВМ, но должно быть предусмотрено, для вычисления, например, погрешности передачи при адаптивных методах приема.

   В зависимости от вида операторов   и  существуют различные методы представления и соответствующие им методы восстановления. Операторы  и  могут быть как линейными, так нелинейными, причем с одним и тем же оператором представления можно использовать разнообразные методы восстановления и наоборот.

   В общем случае линейные операторы имеют вид:

 

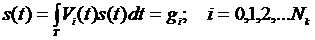    ;                               (2.41)

    tÎT,                              (2.42)

 

где V_i(t), W_i(t) – соответственно весовые и базисные (координатные) функции, выбором которых полностью определяются линейные операторы  и .

   Нелинейные методы дискретного представления и восстановления соответствуют нелинейным операторам  и  в (2.36), (2.37) и включают в себя линейные операторы как частный случай, однако в отличие от линейных мало исследованы и практически не применяются из-за предполагаемой сложности.

   Линейные представления могут быть трех классов:

- представление выборочными мгновенными значениями (точечное);

- дифференциальное (обобщённо-разностное) представление;

- разностное.

 

1.Представление отсчётами (выборочными мгновенными значениями), которое также называют точечным (рис. 2.8).

 

              g_i=s(t_i)=s_i; t_iÎT; i=0,1,...,N_k                                                   (2.43)

 

следует из (1.41), когда весовыми функциями являются дельта - функции.

 

  

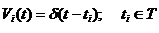
и означает дискретизацию аналогового сообщения с постоянным(T₀=t_i-t_i-1), переменным или случайным шагом, осуществляемую, соответственно, циклическим коммутатором, адаптивным коммутатором или, так называемым, спорадическим (случайным) дискретизаторами.

   Восстановление осуществляется согласно (2.42) в виде усеченного ряда - полинома  степени N_k, который, по отношению к исходному сообщению, называется аппроксимирующим. В частном случае, когда функции W_i(t) выбраны так, что значения аппроксимирующего полинома совпадают со значениями отсчётов (в отсутствие помех):

 

              k = 0,1,...,N_k,                                (2.44)

 

полином  называют интерполяционным (например, полином Лагранжа). Для рассматриваемого вида координат (2.43) интерполяционный полином (2.44) строится на основе базисных функций, относящихся к классу так называемых функций отсчётов, которые обладают следующим общим признаком:

 

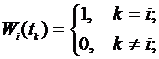              i, k=0,1,...,N_k.                                       (2.45)

2. Дифференциально-разностные представления, при которых очередная формируемая координата g_i выражает отклонение соответствующего отсчета s_i от его экстраполированного значения :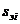

 

                 i>0; g₀=s₀.                        (2.46)

 

   Если предсказание (экстраполяция) делается на основе ранее сформированных координат , то представление называется дифференциальным (обобщенно-разностным) , если же на основе фактических прошлых отсчётов , то представление называется разностным.

 

	S(t)

 

   Дифференциально-разностные представления обычно образуются из первоначального представления отсчётами (т.е. в результате двухступенчатого преобразования аналогового сигнала.

   Восстановление аналогового сигнала выполняется, как правило, также в два этапа: вначале по разностям (2.46) или (2.47) последовательно вычисляются значения отсчётов , затем по полученным значениям строится аппроксимирующий (или интерполирующий) полином .

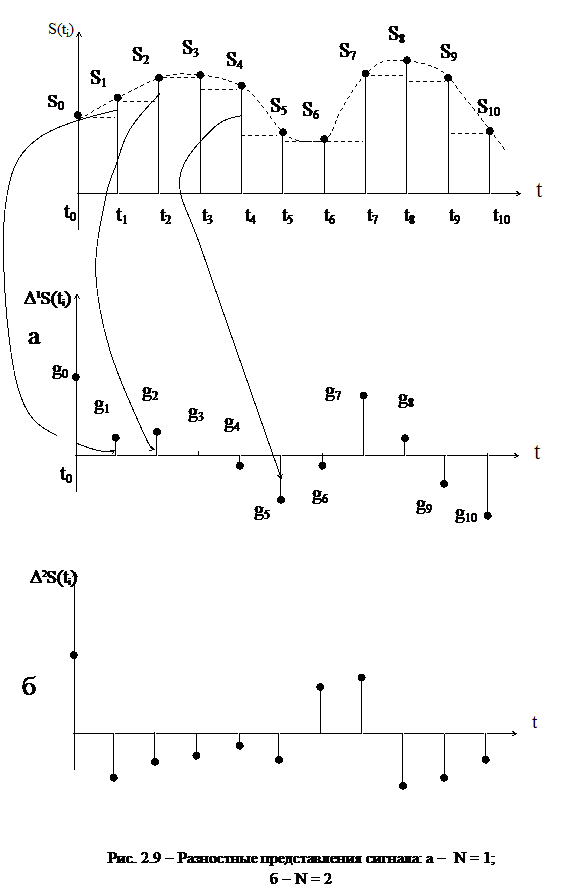
   При разностном представлении порядка N (рис. 2.9) каждая координата g_i, кроме начальной, является конечной разностью образованной обычно из последнего поступившего и  предшествующих отсчётов (такая разность называется восходящей) и имеет вид

 

              i>0; g₀=s₀,     (2.47)

 

 

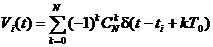              ,                                             (2.48)

 

где 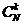- число сочетаний из N по k. Это выражение является частным случаем (2.46) и следует также из (2.41), когда весовые коэффициенты являются линейными комбина-циями функций Дирака (дельта-функций).

   Разностное представление первого порядка (N = 1), согласно (2.41), определяется формулой

 

                                             (2.49)

 

    Формирование сигнала при этом поясняется на рис. 2.9,а.

При N = 1

 

                                           (2.50)

 

   На рис. 2.9,б представлено формирование разностного сигнала при N = 2.

   Для дифференциального представления, в соответствии с (2.46) и (2.47), заменяя  на 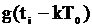, получаем следующее выражение:

 

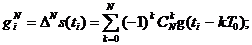              i>0; g₀=s₀.                                  (2.51)

При N = 1

 

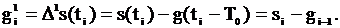                                   (2.52)

 

При N = 2

 

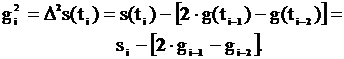                                  (2.53)

   На рис.2.10 представлены принципы формирования дифференциального сигнала при N = 1 (рис.2.10,а) и N = 2 (рис.2.10,б).

   3. Интегральные представления, при которых весовая функция V_i(t), в отличие от предыдущих представлений, не содержат дельта-функций, и представление (2.41) действительно сохраняет интегральный характер. В качестве весовых обычно используются различные системы ортогональных (на интервале Т) функций: степенных (например, полином Лагранжа, Чебышева), тригонометрических и др.

   Координаты g_i являются коэффициентами соответствующего ряда (например, тригонометрического ряда Фурье, ортогонального канонического ряда), построенного по выбранной системе базисных функций, при этом обычно W_i(t)=V_i(t).

   Восстановление аналогового сигнала выполняется в форме усеченного ряда (2.42) с подстановкой в него полученных (переданных) координат .

 

 

 

 

   Интегральные представления называют также обобщенными дискретными. Их главный недостаток - задержка начала формирования, а следовательно, и передачи

координат на время Т, в отличие от двух первых классов представления реализуемых в реальном масштабе времени.

   Из-за этого недостатка интегральные представления практически не применяются.

---

Дата добавления: 2018-02-15; просмотров: 1187; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!