Оценка прочности элементов конструкций
При длительном действии статической нагрузки
Утрата работоспособности элементами теплонапряженных конструкций при длительном действии статической нагрузки происходит, главным образом, по двум причинам:
– вследствие накопления чрезмерно больших деформаций, приводящих к недопустимым по условиям работы перемещениям; такая ситуация характерна дляразрушения вязкого типа;
– физического разрушения (в смысле разделения на части) объекта.
При оценке работоспособности конструкций в рассматриваемых условиях определяют несколько видов фактического коэффициента запаса, сопоставляя их затем с соответствующими нормативными значениями.
1. Коэффициент запаса по перемещениям. Решением задачи ползучести находят нагрузку [Q], при которой зазаданное время эксплуатации реализуется определенное (допустимое) перемещение [u] (Q – действительная или обобщенная нагрузка). Относя ее к рабочей нагрузке Qраб, вычисляют коэффициент запаса по перемещениям
.
Условие работоспособности, которое в данном случае уместно назвать условием жесткости, выглядит вполне традиционно:
nd³[nd],
причем нормативное значение [nd] @ 1,15…1,3 относительно невелико.
Примером использования такого подхода служит расчет рабочей лопатки газотурбинного двигателя, у которой в результате ползучести под действием высокой центробежной нагрузки может быть выбран радиальный зазор между ротором и аэродинамическими уплотнениями в корпусе двигателя (для повышения КПД его стараются сделать как можно меньше).
|
|
|
Для ознакомления с теорией и методами решения подобных задач рекомендуется монография Ю.Н. Работнова «Ползучесть элементов конструкций», в которой рассматриваются расчеты стержней при осевом нагружении и изгибе, пластин, оболочек, труб и других объектов в условиях ползучести.
2. Разумеется, широко используется и привычный коэффициент запаса по напряжениям
;
здесь 
– минимальное значение предела длительной прочности; s max –наибольшее значение нормального, касательного или эквивалентного напряжения. Напомним, что в случае распределения случайной величины (в данном случае предела длительной прочности) по нормальному закону ееминимальное гарантированное с вероятностью 0,997 значение будет равно 
,где 
– математическое ожидание; – среднеквадратическое отклонение.
Если разрушение носит хрупкий характер, необходимо учитывать концентрацию напряжений, причем расчет производится по начальным напряжениям. В случае вязкого разрушения расчет в известной мере условен, поскольку в этих условиях заметную роль начинает играть пластическая составляющая неупругой деформации. Величину нормативного коэффициента запасаназначают в пределах [ns] = = 1,2…2,0.
|
|
|
3. Коэффициент запаса по долговечностиопределяют в терминах времени:
где tf – время до разрушения элемента, определяющего долговечность конструкции в целом; tраб – расчетный ресурс объекта; 
– повреждение, накопленное в течениеnрабочих режимов наиболее нагруженным элементом. При линейном однородном напряженном состоянии время до разрушения, как известно, связано с пределом длительной прочности уравнением кривой длительной прочности(5.4)
,
откуда следует связь коэффициентов запаса по долговечности и напряжению:
,
таким образом,[nt] = 3…5[ns].
4. И, наконец, для конструкций, работающих в рассматриваемых условиях, вводится довольно специфический запас –запас потемпературе:
,
где Tf – минимальное значение температуры, при которой произойдет разрушение наиболее напряженного элемента под действием рабочих усилий;Tраб– максимальнаятемпература эксплуатации. Типичные значения запаса по температуре nT= 40…50° по сравнению с рабочими температурами подобного оборудования невелики.
С учетом термомеханического характера воздействия на элементы теплонапряженных конструкций нормативные значения допускаемого напряженияопределяются как условием прочности, так и условием жесткости. В табл. 5.8 приведены условия выбора допускаемого напряжения для групп теплостойких сталей, применяемых в производстве теплоэнергетического оборудования – котельных, бойлеров, трубопроводов, запорной арматуры и др.– в соответствии с нормами Госгортехнадзора (Котлонадзора).
|
|
|
Таблица 5.8
Условия выбора допускаемого напряжения для групп теплостойких сталей, работающих при повышенных температурах
| Группа материала | Температура эксплуатации, не выше, °С | Допускаемое напряжение |
| Углеродистые стали | 400 | 
|
| Легированные стали | 450 | то же |
| Аустенитные стали | 525 |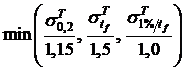 
|
Энергетическое оборудование отличается весьма продолжительными сроками службы, исчисляемыми десятками лет. В расчетах на длительную прочностьприходится использовать деформационные и прочностные характеристики,отвечающие максимум 1×105часам (примерно 11,4 года – провестииспытания на большей временной базе попростунереально); тогда предел ползучести 
= s1/100000. Припеременной температуре подсчитывают эквивалентное допускаемое напряжение
;
здесь[s ]1 – допускаемое напряжение для режима, принятого в качестве базового (обычно, наиболее длительного, стационарного режима); 
– расчетный срок службы;ti– промежуток времени, в течении которого температураTiизменяется не более, чем на 5…10°, и ее можно считать постоянной.
|
|
|
Если говорить об оборудовании, поставляемом на экспорт, то обязательным условиемдопуска на зарубежные рынки является его сертификацияв
соответствии с национальными стандартами, именуемыми Кодами. Одним из наиболее авторитетныхв области продукции энергетического машиностроения является Boiler&PressureVesselCodeASME*, касающийся сосудов давления и других объектов теплоэнергетики.В свою очередь, поставляемое в Россию импортное оборудование подобного назначения проектируется в соответствии с теми же стандартами. Условие выбора допускаемого напряжения согласно BoilerCode’увыглядит следующим образом:
 ;
| (5.16) |
индексом «min»обозначены минимальные значениясоответствующей величины, а верхним индексом «T»–их значения при рабочейтемпературе.
Ниже приведен примервыбора допускаемого напряжения [s ] по BoilerCode’у для жаропрочной стали 1Х13 при температуре 450°С,обладающей следующимимеханическими характеристиками (напряжения заданы в мегапаскалях):
при 20°С – s 0,2 = 460, s В = 630;
при 450°С – s 0,2 = 370, s В = 480, s 1×10-5 = 105, s 1000 = 300, s 100000 = 220.
Полагая, что заданные значения характеристик прочности и ползучести представляют их математическое ожидание и приняв для среднеквадратических отклонений предела текучести, предела прочности и длительной прочноститипичные соотношения: 
=0,1s 0,2; 
= 0,05s i, рассчитаем минимальные гарантированные величины 
= 460 – (3×0,1×460) = 322; 
= 630– (3×0,05×630) = 535,5; 
= 220 – (3×0,05×220) = 187. Согласно условию (5.16)
Порядок расчетов на жесткость и прочность в условиях длительного нагружения продемонстрируем на примере простой стержневой конструкции (рис. 5.25, а). Пусть марка материала, длина и площадь поперечных сечений стержней, предел ползучести для двух скоростей ползучести, а также все традиционные механические характеристики, которые обычно приводятся в справочниках,известны. Необходимо определить
1) в результатерасчета на жесткость – нагрузку FD, если перемещениеD абсолютно жесткого бруса через tв часов работы конструкцииизвестно;
2) в результатерасчета на прочность – нагрузку Ff, еслиизвестно, что через tfчасов работы произошло разрушение конструкции.
Очевидно, рассматриваемая стержневая конструкция (их принято называть фермами) являетсяодин разстатически неопределимой. Раскрытие статическойнеопределимости методом сил или методомперемещений в предположении работы систе мы в пределах упругости, как это принято в сопротивлении материалов, совершенно неоправданно: при длительном нагружении с участием ползучести происходит существенное перераспределение усилий, в чем можно убедиться, анализируя изменение коэффициентов концентрации напряжений и деформаций в области надрезов (см. табл. 5.6). Более того, к моменту достижения предельного равновесия напряжения во всех стержнях станут совершенно одинаковыми, правда для этого необходимо достаточное время.
Таким образом, рассматривая заданную систему заметим, во-первых, что она обладает геометрической и физической симметрией, поэтому усилия(и напряжения) в крайних стержнях будут одинаковы: N1=N3. Поскольку для решения статически неопределимой задачи только лишь условия равновесия недостаточно, необходимо привлечь также условие совместности деформаций(рис. 5.25 б)) и физический закон, связывающий параметры силового и геометрического характера:
условие равновесия: 
;
условие совместности деформаций: 
;
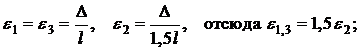
так как 
то скорости деформаций в стержнях будут соотноситься точно так же:
 .
| (5.17) |
В качестве физического используем закон Нортона–Бейли
.
Воспользовавшись двумя заданными значениями предела ползучести
,
определим константы материалаAиn(n> 1).Затем, зная скорости ползучести в стержнях,найдем соответствующие напряжения
,
подставим их в условие равновесия иподсчитаем искомую нагрузку.
Несколько иное завершениепредполагает расчет на прочность, целью которого является оценка «разрушающей»нагрузки Ff. Определив константы материала Aиn,обратимся вновь к условию совместности деформаций(5.17):
.
Поскольку напряжения в двух крайних стержнях оказались больше, чем в среднем, тоони и достигнут предельного состояния в первую очередь. Этаситуация определяет локальное разрушение конструкции.Учитывая, что после достаточно длительной выдержки(сотни или тысячи часов) напряжения в стержнях будут близки,вскоре, вслед за крайними,разрушится и средний стержень – произойдет глобальноеисчерпание несущей способности системы.
Принимая во внимание сказанное,запишемформулу Хоффа применительно к стержням 1, 3
;
после подстановки их в условие равновесия остается лишь подсчитатьпредельную»нагрузку Ff.
В заключение этого раздела приведем некоторые конструктивныеи технологическиемероприятия, с помощью которых добиваются повышения длительной прочности теплонапряженных конструкций.
Дата добавления: 2018-02-15; просмотров: 746; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!