Деформационные характеристики ползучести

Nbsp;

ПРОЧНОСТЬ ПРИ ДЛИТЕЛЬНОМ нагружениИ

В этом, заключительном, разделе мы обсудим эффекты и закономерности, проявляющиеся в ходе экспериментальных исследований металлических материалов, математические модели, описывающие их деформационные и прочностные свойства, а также методы расчета на прочность элементов конструкций, работающих при повышенных температурах и сравнительно медленном изменении нагрузки.В этих условиях (соответствующий вид нагружения принято называть длительным) существенное влияние как на деформационные, так и на прочностные свойства сталей и сплавов оказывает ползучесть – изменение неупругой(вязкой) деформации с течением времени.

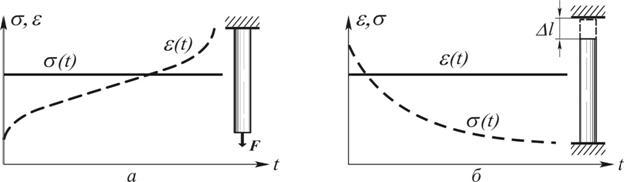
Различают вязкое деформирование в режиме чистой ползучести, когда напряжение со временем не изменяется (s = const), по крайней мере, до момента потери устойчивости пластического течения, проявляющееся в виде образования шейки на образце – рис. 5.1, а и в режиме чистой релаксации, когда неизменной остается деформация (e = const) – рис. 5.1, б; на нем показана схема испытания в так называемых «жестких захватах». Разумеется, возможен и промежуточный между этими двумя «крайностями» процесс.

Механизмы ползучести

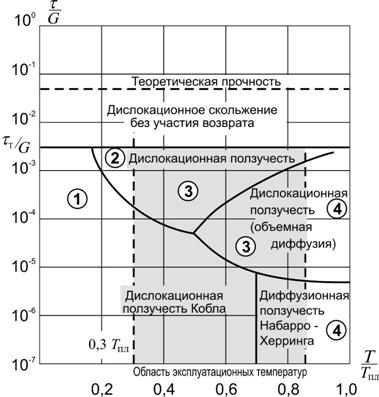
Интенсивность ползучести обычно характеризуют ее скоростью ,которая зависит от целого ряда факторов: напряжения, температуры, вида напряженного состояния, накопленной деформации, химсостава и др. В зависимости от величины каждого или их сочетания может реализовываться тот или иной механизм ползучести. На рис. 5.2 приведена карта механизмов ползучести технически чистого никеля, определяемых величиной касательного напряжения tи температуройТ (t _Т – предел текучести при сдвиге; G – модуль сдвига; Т_пл – температура плавления).Рассмотрим особенности процесса ползучести в каждой из выделенных областей Карты.

Область обратимой ползучести.Характеризуется сравнительно низкими напряжениями и невысокими температурами. Неупругая деформация связана с движением атомов различного рода примесей в кристаллической решетке металла. Полная деформация представляет сумму упругой e_e, пластической e_p (мгновенной, склерономной) и вязкой e_c (от английского слова creep) составляющих

e =e_e + e_p+ e_c.

Поскольку напряжения в этой области невелики, пластическая составляющаяe_pнеупругой деформации обычнопренебрежимо мала. Закон изменения деформации со временем имеет вид

;

e ₀, t₀– постоянныематериала в рассматриваемых условиях (рис. 5.3, 1), подлежащие экспериментальному определению. Как видно, после некоторого времени t₀ процесс накопления деформации прекращается, а после снятия нагрузки наблюдается неустановившаяся ползучесть, приводящая кполному исчезновениюнеупругой деформации по истечении определенного времени (говорят, происходитвозврат деформации). Это явление получило названиевязкоупругости. С нимсвязано внутреннее трение в материале (и определяемое последним рассеяние энергии – гистерезис) при повторно-переменном нагружении в пределах макроупругого по ведения материала.

Область низкотемпературной (логарифмической) ползучести.Изменение деформации со временем описывается законом

(e ₀, n – также постоянные материала в рассматриваемых условиях), что иопределило ее название (рис. 5.3, 2).Как и в предыдущем случае после снятия нагрузки реализуется неустановившаяся ползучесть, полностью прекращающаяся со временем:

Область высокотемпературной ползучести (ползучесть Андраде). Этот механизм ползучестиноситимяЭдварда Невиля да Коста Андраде*,который в 1910году опубликовал результаты экспериментальных исследований закономерности ползучести при средних и высоких напряжениях и температурах, превышающих (0,4…0,5) Т_пл(рис. 5.3, 3),

Таким образом, величина k в пределе пред ставляет минимальную скорость установившейся ползучести (рис. 5.4).Следует отметить, что ползучесть в этом режиме может приводитьк накоплению весьма значительной деформации (десятки и сотни процентов), как правило, недопустимой с точки зрения работоспособности технологического оборудования и рабочих машин.

Примечательно, что полученные еще в начале прошлого века результаты и по сей день не утратили своего значения, поскольку именно к этой области относятсяусловия работы подавляющего большинства современных теплонапряженных конструкций.

Область высокотемпературной диффузионной ползучести. Охватывает диапазон температур, приближающихся к температуре плавления конструкционных сталей и сплавов (Т ≥ 0,8 Т_пл). Для нее, как и в предыдущем случае, характерна высокая нагруженность и, как следствие, накопление больших деформаций, следующих закону

Обратите внимание, что в период действия постоянной нагрузки (s= = const) реализуется установившаяся ползучесть с постоянной скоростью, 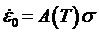линейно зависящей от напряжения (рис. 5.3, 4). К данному типу ползучести склоннылитые мелкозернистыеструктуры.

В реальных условиях обычно реализуются несколько механизмов ползучести, но один из них является преобладающим.

Деформационные характеристики ползучести

Деформационные и прочностные свойства материалов при повышенной температуре получают в ходе испытаний стандартных образцов. Их форма и размеры, испытательное оборудование и регистрирующая аппаратура, а также порядок проведения испытаний и обработки результатов регламентируются соответствующими нормативными документами –ГОСТ 3248-81 (испытания на ползучесть) и ГОСТ 10145-81 (испыта ния на длительную прочность).

Схема испытания на ползучесть при изотермическом «мягком» нагружении показана на рис. 5.1, а. По данным испытаний строят кривые ползучести, схема которых приведена на рис. 5.5, а также находят пределы ползучести– напряжения, соответствующие определенным скоростям ползучести. С их помощью могут быть построены реологическая функция материала – зависимость скорости установившейся ползучести от напряжения и температуры – и изохронные кривые деформирования – аналогитрадиционной кривой деформирования при ряде значений температуры и длительности нагружения(рис. 5.6). Процедуру получения этой характеристики будет рассмотреначуть позже.

Определяющие функции и константыматериала:реологическая функция,предел ползучести и изохронная кривая.Как уже было сказано, реологическая функция– зависимость скорости установившейся ползучести от напряжения и температуры– представляет одну из основных деформационных характеристик материала при повышенной температуре. Для конкретного материалаее формулировка может быть получена в результате обработки кривых ползучести. На рис. 5.5 схематично представлены соответствующие диаграммы в осях «деформация e~ время t» при напряженияхs_iразличной величины. На них отчетливо (за исключением кривых, отвечающих весьма высоким значениям s ) выделяется этап неустановившейся ползучести (I), на котором происходит снижение скорости ,сопровождающее стабилизацию процесса; участокII – фаза стационарной (установившейся) ползучести, где минимальная величина остается постоянной и, наконец, фазаIII – предразрушения, на протяжении которой скорость ползучести вновь возрастает вплоть до потери устойчивости процесса неупругого деформирования. Для математического описания скорости ползучести наII этапе используют функции различного вида, например,

Так реологическая функция жаропрочного никелевого сплава ЭИ 826 ВД (ХН70ВМТЮФ), полученного вакуумно-дуговым переплавом,выглядит следующим образом:

Частным случаем этой зависимости является известный закон Нортона-Бейли

(5.1)

(А_Т – постоянная, отвечающая температуре Т).

Предел ползучестиопределяют различными (в том числе, и по точности) способами, что нашло отражение в его обозначении (приведены в порядке убывания точности):

– напряжение, при котором скорость установившейся ползучести составляет процентов в час;

– напряжение, при котором деформация ползучести достигает d % за tчасов; параметр tобычно назначают кратным 10ⁿ часам:10²,10³,…;

–напряжение, при котором деформация e_f % в момент разрушения была достигнута за t_fчасов.

Показатель степени nпри напряжении s в законе Нортона-Бейли может быть найден как тангенс угла наклона зависимости ,изображенной в двойной логарифмической системе координат (рис. 5.7),

Логарифмируя это выражение, нетрудно определить величину n, а затем и константу А.

В ряде случаев учитывают зависимость показателя степени от времени:

n (t) = a + b t

или осредняют его величину и в дальнейшем считают постоянной –n (t) = n_ср.

Вернемся к изохронным кривым,которые при заданной температуре представляют кривые деформирования, отвечающие ряду значений (10², 10³, 10⁴, …часов) длительности нагружения(рис. 5.6).Учитывая, что в рассматриваемых условиях деформация может исчисляться десятками и сотнями процентов, более корректным представляется запись соответствующих зависимостей в терминахлогарифмической деформации e = ln (1+e) (см. подраздел 1.1).

Рассмотрим способ описание изохронных кривых, предложенный в свое время академиком Ю.Н. Работновым. Этот способопирается на экспериментально установленное свойство их подобия, носит эмпирический характер и, хотя и не отличается особой точностью, зато прост и нагляден.

Среди семейства изохронных кривых выделяют одну,какую – безразлично, принимая еев качествебазовой. Чаще всего это уже знакомая статическая кривая, полученная при такой скорости деформирования, при которой ползучесть не успевает проявиться, т. е., достаточно высокой. В этом случае ее называют «мгновенной»:

s = f₀(e)–

– базовая кривая, соответствующая времени t₀=0.

Будем использовать аппроксимацию как базовой, так и всех остальных кривых степенной зависимостью вида

Напряжение, принадлежащее изохронной кривой с параметром длительности t, определяется по Работнову с помощью базовой, в частности, «мгновенной» кривой деформирования:

(5.2)

где а,bявляются постоянными материала приданной температуре.

Как видно, в этом случае такназываемый коэффициент прочности становится функцией времениK^*= K^*(t). Строго говоря, показатель упрочнения m₀также изменяется со временем, однако данным подходом это не учитывается.

Зная базовую кривую, нетрудно получить деформацию, отвечающую напряжению s с изохронной кривой заданной длительностиt,

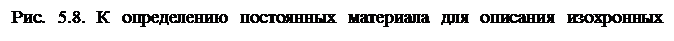
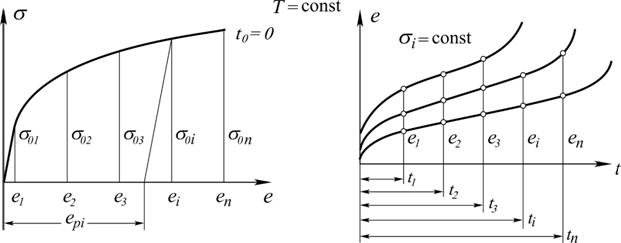Для идентификации этой модели с конкретным материалом необходимо определить постоянные материалаа,b,привлекая базовую кривую деформирования и семейство кривых ползучестиe(s_i)(рис. 5.8), вместо которых с тем же успехомможно воспользоваться зависимостью скорости ползучести от напряжения, например, (5.1), при данной температуре.

Из выражения (5.2) следует

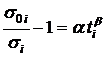где s₀_i– значение напряжения, снятое с базовой кривой; s_i– напряжение, относящееся к изохронной кривой (рис. 5.9).Соответствующая ему деформация e_iпредставляет сумму упругой e_ei, мгновенной пластической e_piи накопленной за время t_i вязкой e_ci составляющих.Таким образом, условие подобия изохронных кривых принимает вид

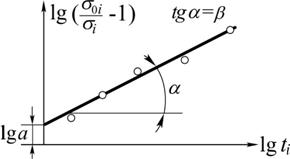
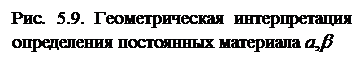очевидно, функция представляет коэффициент подобия в рамках рассмотренного подхода.

Дата добавления: 2018-02-15; просмотров: 1576; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!