Математические модели длительной прочности
Далее рассмотрим модели, описывающиедва качественно различныхмеханизма разрушения –вязкого и хрупкого. Разрушение вязкого типа сопровождается потерей устойчивости неупругого деформирования с образованием шейки на образце;наблюдается при сравнительно высоких значениях нагрузки, чем и определяется относительно небольшойресурс объектов, эксплуатирующихся в подобных условиях.
Модель идеального вязкого разрушения Хоффа.Пустьк стержню постоянного поперечного сечения S0приложена осевая силаF, под действием которой в 
начальный момент времени в любой точке стержня возникает напряжение s 0 (см. рис. 5.1, а).Для актуального* уровня нагрузок пластической e pи упругой e eсоставляющими деформации по сравнению с вязкой ec в первом приближении можно пренебречь. Напомним, если общая деформация превышает 10 %, следует использоватьлогарифмическую деформацию (при таком значении она отличается от обычной инженерной деформации примерно на 5%; дальше различие между ними становится все больше и больше).
Определим время до разрушенияtfстержня. С учетом принятого допущения ресурс пластичностиe cf в данных условияхопределяется интегралом
.
В процессе неупругого деформирования должно выполняться условие неизменности объема
.
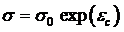Продифференцировав его по времени, получим
.
Сравнивая это выражение с предыдущим, заметим, что 
; с учетом определения 
перепишем последнее выражение – 
, откуда выразим 
, а затем проинтегрируем это уравнение по напряжению от начального значения s 0 до величины s fв момент разрушения
.
Задав скорость ползучести с помощью закона Нортона–Бейли (5.1), получим
.
Определение предельного напряжения в процессе потери устойчивости неупругого деформирования представляет весьма непростую задачу.Из предположения обидеальном вязкомхарактере разрушенияследует, что s f= ∞, то есть,предельному сужению шейки соответствует площадьS=0, по сути, шейка превращается в острие иглы (см. схему на рис. 5.10).
 .
| (5.3) |
В этом случае интегрирование последнего выражения уже не представляет трудности:
Данное соотношение носит название формулы Хоффа. Ее компактная форма имеет вид
;
с другой стороны, 
Таким образом, ресурс пластичности при чисто вязком разрушении определяется величиной, обратной показателю степени в законе Нортона–Бейли.
При болеезначительных нагрузкахs 0, помимо вязкой, необходимо учитывать также начальную пластическуюсоставляющуюнеупругой деформации, которую в целом зададим в виде
(предполагается, что кривая статического деформирования аппроксимирована по Рамбергу–Осгуду степенной функцией
).
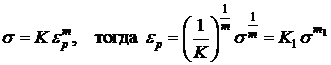Упругой составляющей деформации по-прежнему можно пренебречь.
Проделав аналогичные проделанным выше выкладки, получим
.
Анализ этого выражения показывает, что сомножитель в квадратных скобках близок к единице, то есть, и в этом случае время до разрушения не слишком отличается от прогноза долговечности по формуле Хоффа (рис. 5.10). Как видно, ему соответствует погрешность «не в запас», хоть и не очень большая, ввиду существенно нелинейного характера зависимости скорости ползучести от времени выдержки.
Модель идеального хрупкого разрушения Л.М. Качанова.Хрупким разрушение такого типа называют потому, что оно является практически бездеформационным,сколь либо выраженной шейки на образце ненаблюдается; образование и развитие микротрещин и микропор происходит преимущественно по границам зерен (говорят: носит интеркристаллитный характер); накопление вязкой деформации со временем может прекращаться. Хрупкое разрушение характерно для невысоких уровней нагрузки и, соответственно, продолжительного времени работы.
Пусть расчетная схема остается прежней(см. рис. 5.1, а). Введем скалярный безразмерный неубывающий параметр повреждение 
(Sпор – площадь, занимаемая порами; S0 – исходная (начальная) площадь сечения). Момент разрушения определяется достижением текущего повреждения критического значения П = 1. Это означает, что разрушение произойдет в тот момент, когда поры (несплошности) заполнят всесечение полностью,аистинноенапряжение 
станетравным 
;здесь 
– площадь «живого» сечения.
Разумеется, в действительности этослучитсягораздо раньше – как только напряжение 
достигнет предельнойвеличины.
Поскольку в процессе выдержки нормальная сила в сечениях не меняется, условие равновесия очевидно:
.
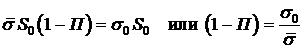Продифференцировав последнее выражение по времени, получим
,
где 
– так называемая функция повреждаемости, определяющая скорость накопления повреждения в зависимости от нагрузки, температуры, вида напряженного состояния, текущего повреждения и других параметров состояния. Преобразуем результат дифференцирования:
,
что после интегрирования по параметру текущего напряжения приводит к равенству
.
На основании экспериментальных данныхфункцию повреждаемостичасто аппроксимируют степенной зависимостью вида
.
После подстановки функции Фв такой формулировке в подынтегральное выражение и выполнении операции интегрирования, получим
 .
| (5.4) |
или, в иной форме,
Величинаs0 представляетпредел длительной прочности – одну избазовыххарактеристик длительнойпрочности материала; общепринятое обозначение которой– 
. Таким образом, предел длительной прочности – такоеначальноенапряжение, при котором при температуре T за t часов произойдет разрушение материала в условиях линейного напряженного состояния.
Модели Хоффа и Качанова представляют идеализированноеописание закономерностей вязкого и хрупкого разрушения и делают они это, если так можно выразиться, предельно контрастно, без полутонов. В реальных же условиях один из механизмов, как правило, является превалирующим, либо оба могут сочетаться в той или иной пропорции. В случае подобного, как говорят,смешаного разрушения оценку долговечности производят с помощьюгипотезы суммирования повреждений 
, отвечающих механизмам вязкого и хрупкого разрушения,во временнόй трактовке
Пв + Пхр= 1;
;
в данном случае гипотеза представлена в варианте линейного суммирования.
Дата добавления: 2018-02-15; просмотров: 542; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!