Кинетическое уравнение повреждаемости. Линейное суммирование повреждений при блочном нагружении
Предположим, что в начальный момент времени t0 = 0элемент объема материала находится в неповрежденном состоянии – П(0)= 0, а при достижении предельного состояния в момент времени t fповреждениестановится критическим – П(tf) = 1. В общем случае, как уже было сказано, скорость повреждения зависит от нагрузки (напряжения), характераего изменения, температуры, вида напряженного состояния, длительности нагружения, текущего повреждения, других параметров состояния и описывается функцией повреждаемости
.
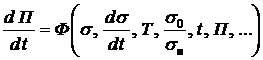Подобного типа выражение представляет кинетическое уравнение повреждаемости. Под повреждаемостью понимается процесс накопления повреждения, которое, в свою очередь, характеризует степень дефектности материала.
Если ограничится частным случаем – чистой ползучестью ( 
) в условиях регулярного (в этом случае нет необходимости вводить параметры времени и накопленного повреждения) изотермического (T=const) одноосного растяжения ( 
), то задачасущественно упрощается:
,
так как Ф становится функцией всего лишь одного аргумента. Условие разрушения приобретает вид
.
Определив тем или иным способом вид функции повреждаемости и зная закон изменения s (t), можно найти время до разрушения tf.
В результате испытаний на длительную прочность (рис. 5.11) получают зависимость вида (5.4)
 ,
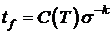| (5.5) |
представляющую уравнение кривой длительной прочности.Используем функциюповреждаемостивида 
в качестве подынтегральноговыражения:
|
|
|
;
это соотношение носитназвание интеграла Бейли.
При неизменном в процессе нагружения напряжении данный интеграл превращается, по сути, в тождество
;
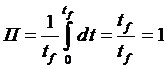если же напряжение со временем изменяется, то подстановка уравнения кривой ползучести (5.5) позволяет,выполнив интегрирование, определить время до разрушения tf.
Рассмотрим более подробно второй вариант. Для бóльшей наглядности монотонное плавное изменение напряжения s (t) заменим кусочно-постоянной зависимостью, такой, что на каждом отрезке времени D ti напряжениеsi=const; очевидно S D ti =tf (рис. 5.12).Как известно, любой интеграл может быть представлен суммой интегралов:
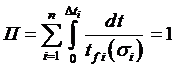
или 
–
– правило линейного суммирования повреждений во временнόй трактовке, или закон Робинсона.Следует отметить, что это правило распространяется и на случай переменной температуры:
 .
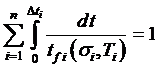| (5.6) |
Шаг дискретизации по температурепринимаютD T =5…10°– в зависимости от скорости изменения температуры и интенсивности процессов ползучести и повреждаемостипри температуре Ti.
Пример 5.1.Определить время до разрушения стержня, подверженного действию осевой растягивающей силы в условиях термомеханического блочного нагружения (рис. 5.13, а).
|
|
|
Воспользуемся законом Робинсона, который в данном случаеследует записать в виде
.
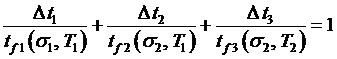Длительности tfi(si, Ti) определяются с помощью кривых длительной прочности (рис. 5.13, б).
Представим каждый отрезок времени Dt i как долю общего ресурса:
;
откуда долговечность для заданной программы нагружения определяется величиной, обратнойсумме слагаемых в скобках.
Помимо суммирования повреждений во временнόй трактовкев литературе обсуждаются и другие подходы к осуществлению этой процедуры. К ней приходится прибегатьв случае нерегулярного, в частности, блочного нагружения. Широкое распространение как в научной, так и в инженерной практике получила гипотеза линейного суммирования повреждений в деформационной трактовке, согласно которой повреждение определяется в терминах деформаций – инженерной или логарифмической:
.
Экспериментальные проверки показали, что такой подход позволяет получить более точную по сравнению свременнόй трактовкой оценку длительной прочности конструкции.
Из сказанного следует, что определение ресурса пластичности (предельной деформации в момент разрушения) в условиях вязкого деформирования имеет важное практическое значение.
|
|
|
Дата добавления: 2018-02-15; просмотров: 649; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!