Вопрос 16) Уравнение прямой, проходящей через заданную точку в заданном направлении. Уравнение прямой, проходящей через две заданные точки. Уравнение прямой в отрезках.
Уравнение прямой, проходящей через данную точку в данном направлении.
Предположим, что прямая проходит через точку M1 (x1,y1) и образует с осью OX угол . Составим уравнение этой прямой.
Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg . Возьмем произвольную точку M (x , y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M1 лежат на прямой, то их координаты удовлетворяют уравнению прямой:
y = k · x + b ,
y1 = k · x1 + b .
Вычитая эти равенства, получим:
y - y1 = k · (x - x1) - уравнение прямой, проходящей через данную точку в данном направлении.
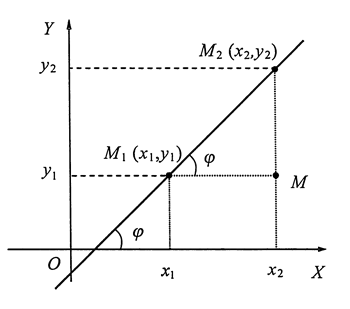
Даны две точки M1(x1, y1) и M2(x2, y2). Составим уравнение прямой, проходящей через две эти точки.
Из треугольника M1M2M:
,
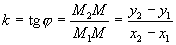- угловой коэффициент прямой, проходящей через две данные точки.
Воспользуемся уравнением прямой, проходящей через данную точку M1 и в данном направлении 
:
Если точки имеют различные абсциссы и ординаты, то, умножая обе части последнего равенства на величину
,
получим
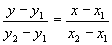- уравнение прямой, проходящей через две данные точки.
Если точки имеют одинаковые абсциссы или одинаковые ординаты, то используют формулу 
.
Предположим, что прямая отсекает на осях координат отрезки a и b единиц соответственно.
Соответствим уравнение этой прямой. Используем уравнение прямой, проходящей через две данные точки A(a,0) и B(0,b).
|
|
|
Вопрос 17) Угол между прямыми. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых.
Определение. Углом между двумя прямыми I и II называется угол, отсчитываемый в положительном направлении от прямой I к прямой II.
Пусть даны две прямые, заданные уравнениями с угловыми коэффициентами
y = k1 · x + b1, y = k2 · x + b2.
Найдем угол между первой и второй прямыми. Обозначим углы наклона прямых и . Тогда
k1 = tg, k2 = tg2.
Проведем через точку пересечения прямую, параллельную оси OX.
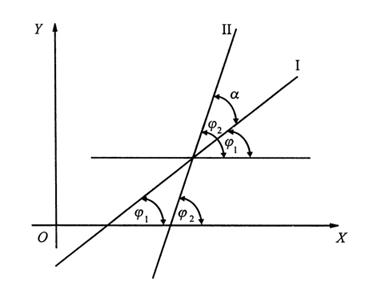
-формула для вычисления угла между двумя пряммыми
1. Предположим, что прямые параллельны:
tg
k1 = k2 - условие параллельности прямых.
2. Предположим, что прямые перпендикулярны:
0 tg не существует ctg = 0
k1 · k2 = -1 - условие перпендикулярности прямых.
Вопрос 18) Окружность. Эллипс.
Окружность.
Определение. Геометрическое место точек, расстояние от каждой из которых до данной точки О, называемой центром, есть величина постоянная, называется окружностью.
|
|
|
= R – каноническое уравнение окружности
Окружность является частным случаем эллипса, когда большая и малая полуоси равны, с = 0, фокусы сливаются в центр. Эксцентриситет окружности равен нулю.
.
Эллипс.
Определение 1. Геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется эллипсом.
- каноническое уравнение эллипса.
Исследуем форму эллипса.
1. Найдем точки пересечения с осями.
OX: y = 0, 
;
OY: x = 0, 
;
A(a; 0); B (-a; 0); C (0; b); D (0; -b).
Определение 2. Точки A, B, C, D называются вершинами эллипса.
2. Из вида уравнения следует, что линия симметрична относительно осей OX и OY и начала координат.
3.
Следовательно, кривая расположена в прямоугольнике со сторонами 2а и 2b.
Построим данную кривую.
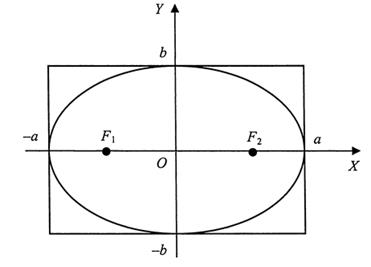
Определение 3. Отношение фокусного расстояния к большой оси эллипса называется эксцентриситетом эллипса.
.
Определение 4. Параметр a называется большой полуосью эллипса, параметр b называется малой полуосью эллипса.
Дата добавления: 2020-01-07; просмотров: 1167; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!