Линейная зависимость векторов
ЛИНЕЙНАЯ АЛГЕБРА ЭКЗАМЕН
Вопрос 1) Вектор. Длина вектора. Скалярное произведение. Угол между векторами. Коллинеарность и ортогональность векторов. Операции над векторами. Линейное векторное пространство.
Опр. Упорядоченная совокупность п действительных чисел а1, а2, …, ап называется п-мерным вектором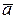 
=( а1, а2, …, ап). Числа а1, а2, …, ап называются координатами вектора.
Геометрически для п>3 вектор изобразить нельзя, однако применить это понятие для практических целей вполне можно. Например, в виде вектора можно представить объем выпуска п видов продукции, цены этой продукции и т.д.
Два вектора называются равными, если равны их соответствующие координаты: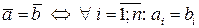 
.
Длиной (нормой) п-мерного вектора 
называется величина
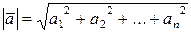
Скалярным произведением двух п-мерных векторов и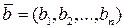 
называется число, равное сумме попарных произведений их координат:
.
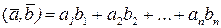Скалярное произведение имеет следующие свойства:
1. 
;
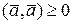2. 
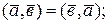
3. 
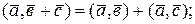
4. 
.
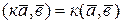Угол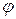 
между двумя п-мерными векторам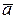и и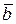 
определяется по формуле:
.
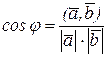Два ненулевых п-мерных вектора и 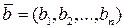называются ортогональными (перпендикулярными), если угол между ними равен 90º. Условием ортогональности векторов является равенство нулю их скалярного произведения.
Два п-мерных вектора и 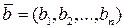называются коллинеарными, если найдется ненулевое число 
, такое, что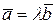 
. Условием коллинеарности векторов является пропорциональность их координат:
|
|
|
.
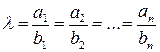Суммой (разностью) двух п-мерных векторов и 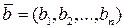называется п-мерный вектор, каждая координата которого равна сумме (разности) соответствующих координат исходных векторов:
.
Произведением п-мерного вектора на число к называется п-мерный вектор, каждая координата которого равна произведению соответствующей координаты исходного вектора 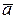на число к: 
.
Свойства операций над векторами.
1. 
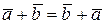- коммутативность суммы
2. 
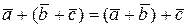- ассоциативность суммы
3. 
- ассоциативность относительно числового множителя
4. 
- дистрибутивность суммы
5. 
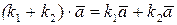- дистрибутивность относительно суммы числовых множителей
6. 
7. 
8. 
.
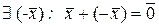Опр. Совокупность всех п-мерных векторов с введенными на ней операциями сложения и умножения на число, удовлетворяющая приведенным выше свойствам, называется линейным векторным пространством (Еп).
Линейное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным свойствам, называется евклидовым пространством.
Единичным п-мерным вектором или ортом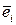 
называется вектор, у которого i-я координата равна единице, а остальные – нулю: 
, 
, …, 
.
|
|
|
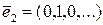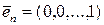Вопрос 2) Свойства систем векторов. Линейная зависимость векторов. Теорема Штейница.
Свойства систем векторов.
Теорема 1. Если система векторов содержит нулевой вектор, то она линейно зависима.
Док-во. Пусть, например,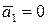 
. Тогда равенство 
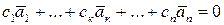справедливо при с1=1, с2=с3=…=сп=0, т.е. при ненулевом коэффициенте с1. Значит, система линейно зависима.
Теорема 2. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.
Док-во. Пусть, например, векторы 
линейно зависимы. Тогда в равенстве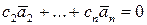 
не все коэффициенты равны нулю. Но тогда при тех же коэффициентах и с1=0 будет справедливо и равенство 
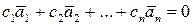. Система линейно зависима.
Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Доказывается «от противного».
Теорема 3 (теорема Штейница). Если каждый из векторов 
является линейной комбинацией векторов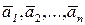 
и m > n, то система векторов линейно зависима.
Следствие. В любой системе п-мерных векторов не может быть более чем п линейно независимых.
Док-во. Каждый п-мерный вектор выражается в виде линейной комбинации п единичных векторов. Поэтому, если система содержит т векторов и т>п, то по теореме Штейница эта система линейно зависима.
|
|
|
Линейное пространство называется п-мерным, если в нем существуют п линейно независимых векторов, а любые п+1 векторов являются линейно зависимыми.
Линейная зависимость векторов
Пусть дана система п-мерных векторов .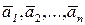
Опр. Линейной комбинацией векторов 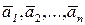называется вектор, равный сумме произведений этих векторов на произвольные действительные числа:
= 
,
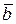где 
- некоторые коэффициенты.
Пример. Составить линейную комбинацию векторов
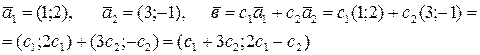
Опр. Говорят, что вектор 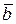разлагается по системе векторов 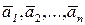, если вектор 
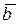можно представить в виде линейной комбинации векторов :
.
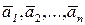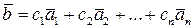Опр. Выпуклой линейной комбинацией векторов 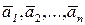называют линейную комбинацию,в которой все коэффициенты неотрицательны, и сумма коэффициентов равна единице.
Опр. Векторы 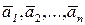называют линейно независимыми, если их линейная комбинация равна нулю только при нулевых значениях коэффициентов:
.
В противном случае векторы называют линейно зависимыми. Т.е. векторы линейно зависимы, если при выполнении равенства
|
|
|
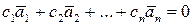
среди чисел найдется хотя бы одно ненулевое.
Пример. Доказать, что векторы 
и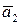 
из предыдущего примера линейно независимы.
Теорема. Система векторов 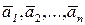является линейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов системы. Верно и обратное утверждение.
Док-во. Пусть линейная комбинация векторов равна нулю, и при этом среди коэффициентов есть ненулевой, например,
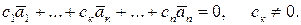
Тогда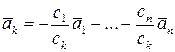 
, т.е. один из векторов системы представлен в виде линейной комбинации других.
Пусть теперь один из векторов равен линейной комбинации других, т.е.
.
(перенесем все в одну часть)
.
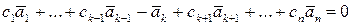Линейная комбинация равна нулю, и при этом не все коэффициенты нулевые, т.е. система линейно зависима.▲
Нетрудно доказать, что различные п-мерные единичные векторы линейно независимы.
Самостоятельно.
Каждый п-мерный вектор может быть представлен единственным образом в виде линейной комбинации единичных п-мерных векторов с коэффициентами, равными координатам вектора
.
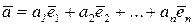Дата добавления: 2020-01-07; просмотров: 252; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!