Вопрос 9) Обратная матрица. Теорема об обратной матрице.
Вспомним свойство чисел:  .
.
Аналог существует для матриц.
Опр. Квадратная матрица называется невырожденной, если ее определитель не равен нулю. В противном случае матрица называется вырожденной.
Опр. Матрица А-1 называется обратной к квадратной матрице А, если их произведение равно единичной матрице:
А·А-1=А-1·А=Е.
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица А-1 существует и единственна тогда и только тогда, когда матрица А невырожденная.
Док-во. Необходимость.
Дано: А-1. Докажем, что  .
.
Имеем по определению: А·А-1=А-1·А=Е. Тогда  . Следовательно,
. Следовательно,  и
и  .
.
Достаточность. Дано:  . Докажем, что существует А-1. Построим ее с помощью следующих действий.
. Докажем, что существует А-1. Построим ее с помощью следующих действий.
1. Транспонируем матрицу А: АТ.
2. Заменим каждый элемент матрицы АТ его алгебраическим дополнением, получим так называемую присоединенную матрицу А*:

3. Разделим все элементы А* на  :
:
 .
.
Покажем, что полученная таким способом матрица является обратной к А.


 ;
;
 .
.
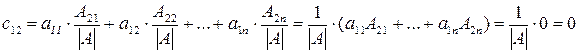 .
.

Таким образом, матрица С является единичной матрицей, а значит матрица  - обратная к А, ч.т.д.
- обратная к А, ч.т.д.
Аналогично доказывается, что А-1А=Е.
Единственность.
От противного. Предположим, что у матрицы А есть две различные обратные матрицы А-1 и  . Имеем: А А-1=Е. Умножим это равенство слева на
. Имеем: А А-1=Е. Умножим это равенство слева на  .
.
 А А-1=
А А-1=  Е,
Е,
ЕА-1=  ,
,
А-1=А. Получили противоречие, доказывающее теорему.▲
Замечание. Теорема не только решает вопрос о существовании обратной матрицы, но и дает алгоритм ее нахождения:
1. Найти определитель матрицы, убедиться, что она невырожденная.
2. Транспонировать матрицу:  .
.
3. Составить матрицу алгебраических дополнений к АТ(присоединенную матрицу) А* .
4. Найти обратную матрицу по формуле  .
.
Существует и другой способ нахождения обратной матрицы, связанный с выполнением над матрицей так называемых элементарных преобразований. К ним относятся:
- умножение любой строки на число, отличное от нуля;
- сложение строк;
- перестановка строк.
Опр. Две матрицы называются эквивалентными, если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.
Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице. Применяя ту же последовательность преобразований к единичной матрице, можно получить обратную матрицу к данной. Обычно элементарные преобразования проводят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой записана данная матрица, а в правой – единичная. С помощью элементарных преобразований в левой части создают единичную матрицу, а в правой автоматически создается обратная матрица.
Пример. Найти обратную матрицу для матрицы 
Решение. Составим расширенную матрицу:

 изменим порядок строк
изменим порядок строк

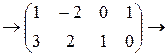 умножим первую строку на (-3) и сложим со второй
умножим первую строку на (-3) и сложим со второй

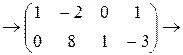 разделим вторую строку на 8
разделим вторую строку на 8

 умножим вторую строку на 2 и сложим с первой
умножим вторую строку на 2 и сложим с первой

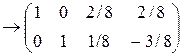 .
.  .
.
Обратные матрицы находят применение, например, в решении матричных уравнений.
Пример. Решить матричное уравнение  ,
,
где А, В, С, Х - квадратные матрицы одинакового порядка, А – невырожденная.
Решение.  ;
;
Умножим это уравнение слева на А-1: 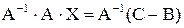 . Получим:
. Получим:
 ;
;
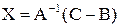 .
.
Дата добавления: 2020-01-07; просмотров: 150; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
