Вопрос 3) Ранг и базис системы векторов. Теорема о представлении вектора в виде линейной комбинации векторов линейно зависимой системы.

Опр. Рангом r системы векторов называется максимальное число линейно независимых векторов системы.

Опр. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.

В частности, любая совокупность п линейно независимых векторов п-мерного пространства является базисом.

Теорема. Любой вектор системы можно единственным образом представить в виде линейной комбинации векторов базиса этой системы.

Док-во. Пусть система имеет базис .

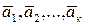1) Пусть вектор 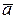из базиса (например, это ). Тогда .

2) Пусть вектор 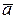не из базиса. Например, это вектор , где р>к.

Рассмотрим систему 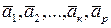.Она является линейно зависимой. Следовательно, найдутся числа , не все равные нулю, такие, что 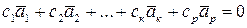. Очевидно, что , т.к. в противном случае базис являлся бы линейно зависимым. Тогда

3) докажем, что разложение вектора по базису единственно.

Предположим противное: имеются два разложения вектора по базису:

Вычитая эти равенства, получим:

Учитывая линейную независимость векторов базиса, получим:

, …, .

Следовательно, разложение единственно.▲

Ранг п-мерного пространства равен его размерности. Значит, любой его базис состоит из п линейно независимых п-мерных векторов. Любая система в п-мерном пространстве, содержащая больше, чем п векторов, линейно зависима. Любой вектор пространства можно однозначно разложить по векторам любого базиса. Коэффициенты разложения называются координатами данного вектора в этом базисе.

Вопрос 4) Ранг и базис системы векторов.

Опр. Рангом r системы векторов называется максимальное число линейно независимых векторов системы.

В частности, любая совокупность п линейно независимых векторов п-мерного пространства является базисом.

Вопрос 5) Матрицы, их виды. Операции над матрицами.

Опр. Прямоугольная таблица, состоящая из т строк и п столбцов действительных чисел называется матрицей размера т×п. Матрицы обозначают заглавными латинскими буквами: А, В,…, а массив чисел выделяют круглыми или квадратными скобками.

Числа, входящие в таблицу, называются элементами матрицы и обозначаются малыми латинскими буквами с двойным индексом , где i – номер строки, j – номер столбца, на пресечении которых расположен элемент. В общем виде матрица записывается так:

Две матрицы считаются равными, если равны их соответствующие элементы.

Если число строк матрицы т равно числу ее столбцов п, то матрица называется квадратной (в противном случае – прямоугольной).

Матрица размера называется матрицей-строкой. Матрица размера

называется матрицей-столбцом.

Элементы матрицы, имеющие равные индексы ( и т.д.), образуют главную диагональ матрицы. Другая диагональ называется побочной.

Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю.

Диагональная матрица, у которой диагональные элементы равны единице, называется единичной матрицей и имеет стандартное обозначение Е:

Если все элементы матрицы, расположенные выше (или ниже) главной диагонали равны нулю, говорят, что матрица имеет треугольный вид:

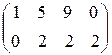
Операции над матрицами.

1. Транспонирование матрицы – преобразование, при котором строки матрицы записывают в виде столбцов при сохранении их порядка. Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали:

2. Матрицы одинаковой размерности можно суммировать (вычитать). Суммой (разностью) матриц называется матрица той же размерности, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц:

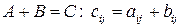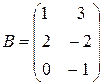
3. Любую матрицу можно умножать на число. Произведением матрицы на число называется матрица того же порядка, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число:

4. Если число столбцов одной матрицы равно числу строк другой, то можно выполнить умножение первой матрицы на вторую. Произведением таких матриц называется матрица, каждый элемент которой равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй матрицы.

Следствие. Возведение матрицы в степень к>1 есть произведение матрицы А к раз. Определено только для квадратных матриц.

Пример.

Свойства операций над матрицами.

1. А+В=В+А;

2. (А+В)+С=А+(В+С);

3. к(А+В)=кА+кВ;

4. А(В+С)=АВ+АС;

5. (А+В)С=АС+ВС;

6. к(АВ)=(кА)В=А(кВ);

7. А(ВС)=(АВ)С;

8. АЕ=ЕА=А;

9. (кА)^Т=кА^Т;

10. (А+В)^Т=А^Т+В^Т;

11. (АВ)^Т=В^ТА^Т;

Перечисленные выше свойства аналогичны свойствам операций над числами. Есть и специфические свойства матриц. К ним относится, например, отличительное свойство умножения матриц. Если произведение АВ существует, то произведение ВА

- может не существовать

- может отличаться от АВ.

Пример. Предприятие выпускает продукцию двух видов А и В и использует при этом сырье трех типов S₁, S₂, и S₃. Нормы расхода сырья заданы матрицей N= , где n_ij – количество сырья j, расходуемого на производство единицы продукции i. План выпуска продукции задан матрицей С=(100 200), а стоимость единицы каждого вида сырья – матрицей 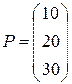. Определить затраты сырья, необходимые для планового выпуска продукции и общую стоимость сырья.

Решение. Затраты сырья определим как произведение матриц С и N:

Общую стоимость сырья вычислим как произведение S и Р:

Дата добавления: 2020-01-07; просмотров: 387; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!