Вопрос 6) Дополнительные миноры и алгебраические дополнения элементов матрицы.

Опр. Минором порядка к матрицы А _{m × n} называется определитель к-го порядка, полученный из матрицы А вычеркиванием (т-к) строк и (п-к) столбцов ( ).

 

Опр. Дополнительным минором М _ij элемента a_ij квадратной матрицы А п-го порядка называется определитель порядка (п-1), полученный из матрицы А вычеркиванием строки и столбца, на пересечении которых стоит элемент a_ij .

Опр. Алгебраическим дополнением A_ij элемента a_ij квадратной матрицы А п-го порядка называется число

.

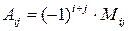Вопрос 7) Ранг матрицы и способы его нахождения.

В математических исследованиях имеет большое значение понятие ранга матрицы.

Пусть дана произвольная матрица размера . Минором к-го порядка М_к называют определитель порядка к ( ), составленный из элементов, расположенных на пересечении любых к строк и к столбцов. Для данной матрицы можно составить   миноров к-го порядка.

Опр.  Рангом матрицы r ( A ) называется наивысший порядок отличных от нуля миноров этой матрицы.

Очевидно, что r ( A ) . Для квадратной матрицы п –го порядка r ( A )= n тогда и только тогда, когда матрица А – невырожденная.

 

Если все миноры к-го порядка данной матрицы равны нулю, то равны нулю и все миноры более высоких порядков (почему? ). Поэтому, если среди миноров к-го порядка есть отличный от нуля минор М_к, а все миноры порядка к+1 равны нулю, то ранг такой матрицы равен к. Это свойство дает нам способ вычисления ранга матрицы.

 

Опр. Отличный от нуля минор порядка r = r ( A ) называется базисным минором матрицы А, а строки и столбцы в которых он расположен, называются базисными строками (столбцами).

Любая строка матрицы является линейной комбинацией ее базисных строк. (То же верно для столбцов). Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы.

При элементарных преобразованиях ранг матрицы не меняется. Можно доказать, что посредством элементарных преобразований любая ненулевая матрица А приводится к треугольной матрице В:

В матрице В вычеркиваем строки, все элементы которых равны нулю, что не изменяет ранга матрицы. Ранг полученной матрицы, состоящей из r строк, равен r, так как минор порядка r в левом верхнем углу отличен от нуля.  Тогда и r(В) = r, т.е. ранг треугольной матрицы равен числу ее ненулевых строк. Матрица В получена из А путем элементарных преобразований, поэтому r(А) = r.

Вывод: для того, чтобы найти ранг матрицы, необходимо с помощью элементарных преобразований привести ее к треугольному виду и подсчитать количество ненулевых строк.

 

Вопрос 8) Определители, их свойства.

Для любой квадратной матрицы А существует число  или det A, называемое определителем, характеризующее эту матрицу. 

Опр. Определителем квадратной матрицы п-го порядка называется число, равное сумме п! слагаемых, каждое из которых является произведением п элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы со знаком “+”или “—” .

 

Так, определителем первого порядка называется само число а₁₁.

 

Определителем квадратной матрицы А второго порядка называется число, определяемое по формуле: .

Правило вычисления этого определителя легко запомнить визуально: из произведения элементов главной диагонали вычитается произведение элементов побочной диагонали матрицы.

 

Определителем квадратной матрицы А третьего порядка называется число, определяемое по формуле:

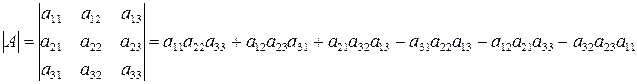Это число представляет собой сумму 3!=6 слагаемых, в которые входят по одному элементу из каждой строки и столбца. Запомнить правило вычисления этого определителя можно, пользуясь схемой, называемой правилом треугольников или правилом Сарруса.

Вычисление определителей порядка больше 3 основано на применении свойств определителей.

 

Свойства определителей.

1. При транспонировании величина определителя не меняется.

Следствие. Строки и столбцы в определителе обладают одинаковыми свойствами.

2. Если все элементы строки определителя умножить на одно число, то значение определителя умножится на это число.

Следствие. Постоянный множитель строки можно вынести за знак определителя.

3. При перестановке двух строк определитель меняет знак на противоположный.

Следствие. Определитель, имеющий равные или пропорциональные строки, равен нулю.

4. Если каждый элемент строки определителя представлен в виде суммы, то определитель равен сумме определителей, у которых в данной строке стоят слагаемые.

5. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц.

6. Определитель треугольной (в т.ч. диагональной) матрицы равен произведению элементов главной диагонали.

7. Определитель равен сумме произведений элементов любой строки на их алгебраические дополнения (т. Лапласа):

- разложение по i-й строке,

- разложение по j-му столбцу.

8. Сумма произведений элементов какой-либо строки определителя на алгебраические дополнения элементов другой строки равна нулю.

при .

 

9. Определитель матрицы не изменится, если к элементам одной его строки прибавить элементы другой строки, умноженной на одно и то же число.

 

---

Дата добавления: 2020-01-07; просмотров: 465; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!