Контрольные  вопросы  и  задания

1. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?

2. Запишите формулы для определения положения центра тя­жести неоднородных и однородных тел, формулы для определения положения центра тяжести плоских сечений.

3. Повторите формулы для определения положения центра тяже­сти простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга.

4. Что называют статическим моментом площади?

5. Вычислите статический момент данной фигуры относительно оси Ox . h = 30 см; b = 120 см; с = 10 см (рис. 8.6).

 

           

6. Определите координаты центра тяжести заштрихованной фигуры (рис. 8.7). Размеры даны в мм.

7. Определите координату у фигуры 1 составного сечения
(рис. 8.8).

При решении воспользоваться справочными данными таблиц ГОСТ «Сталь горячекатанная» (см. Приложение 1).

 

                    

 

 

66                                                      Лекция 9

ЛЕКЦИЯ 9

Тема 1.7. Основные понятия кинематики.  

Кинематика точки

Иметь представление о пространстве, времени, траектории, пути, скорости и ускорении.

Знать способы задания движения точки [естественный и координатный).

Знать обозначения, единицы измерения, взаимосвязь кинема­тических параметров движения, формулы для определения скоро­стей и ускорений (без вывода).

Кинематика рассматривает движение как перемещение в про­странстве. Причины, вызывающие движение, не рассматриваются. Кинематика устанавливает способы задания движения и определяет методы определения кинематических параметров движения.

Основные  кинематические   параметры

Траектория

Линию, которую очерчивает материальная точка при движении в пространстве, называют траекторией.

Траектория может быть прямой и кривой, плоской и простран­ственной линией.

Уравнение траектории при плоском движении: у = f ( x ).

Пройденный путь

Путь измеряется вдоль траектории в направлении движения. Обозначение — S , единицы измерения — метры.

Уравнение движения точки

Уравнение, определяющее положение движущейся точки в зави­симости от времени, называется уравнением движения.

Положение точки в каждый момент времени можно опреде­лить по расстоянию, пройденно­му   вдоль   траектории   от   некоторой   неподвижной   точки,   рассмат-

                                

                    Тема 1.7. Основные понятия кинематики                                    67

риваемой как начало отсчета (рис. 9.1). Такой способ задания дви­жения называется естественным.

Таким образом, уравнение движения можно представить в виде S = f ( t ). Положение точки можно также определить, если известны ее координаты в зависимости от времени (рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения: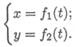

В случае пространственного движе­ния добавляется и третья координата z= f3( t ).

Такой способ задания движения на­зывают координатным.       

                                          

Скорость движения

Векторная величина, характеризующая в данный момент бы­строту и направление движения по траектории, называется скоро­стью.

Скорость — вектор, в любой момент направленный по каса­тельной к траектории в сторону направления движения (рис. 9.3).                

                                       

Если точка за равные промежутки времени проходит равные расстояния, то движение называ­ют равномерным. Средняя скорость на пути  AS определяется как         

 где AS — пройденный путь за время Д*; At — промежуток времени.

Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным.

В этом случае скорость — величина переменная и зависит от времени v = f ( t ).

При рассмотрении малых промежутков времени (∆ t —► 0) сред­няя скорость становится равной истинной скорости движения в дан­ный момент. Поэтому скорость в данный момент определяют как

68                                                      Лекция 9

 

производную пути по времени:

                                                          

За единицу скорости принимают 1 м/с. Иногда скорость измеряют в км/ч,

          1000
1 км/ч = ------ = 0,278 м/с.

                3600

Ускорение точки

Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.

Скорость точки при перемещении из точки М 1 в точку M 2 ме­няется по величине  и  направлению. Среднее  значение  ускорения  за   этот  промежуток       

                                     

При рассмотрении бесконечно ма­лого промежутка времени среднее ускорение превратится в ускорение в  данный момент:

                                                              

Обычно для удобства рассматривают две взаимно перпен­дикулярные составляющие ускорения: нормальное и касательное (рис. 9.5).

Нормальное ускорение а_п характеризует изменение скорости по направлению и определяется как

         

где г — радиус кривизны траектории в данный момент времени.

Нормальное ускорение всегда направлено перпендикулярно ско­рости к центру  дуги.

Касательное ускорение  аt   характеризует  изменение  скорости  по величине  и  всегда   направлено   по  касательной  к  траектории;  при ускорении   его   направление   совпадает  с   направлением   скорости,  а

              Тема 1.7. Основные понятия кинематики                                     69

при замедлении оно направлено противоположно направлению век­тора скорости.

Формула для определения касательного ускорения имеет вид:

            

Значение полного ускорения определяется как
                                                                                    (рис. 9.6).                                                                                                                               

 

 

Примеры решения задач

Пример 1. Дано уравнение движения точки: S = 0,36t² + 0,18t. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые 3 секунды.

Решение

Пример 2.

Точка движется по кривой радиуса r = 10 м со­гласно уравнению S = 2,5t² + 1,2t + 2,5 (рис. 9.6).

70                                                                         Лекция 9

Определить полное ускорение точки в конце второй секунды движения и указать направление касательной и нормальной соста­вляющих ускорения в точке М.

Решение

                                                               d v

     1.  Касательное ускорение определяется как at = —.

dS                              d t

   Уравнение скорости: v = ---- .

dt

  Скорость будет равна v = 2 • 2,5 t + 1,2; v = 5 t + 1,2 (м/с).

Касательное ускорение: at = v' = 5 м/с² .

Вывод: касательное ускорение не зависит от времени, оно по­стоянно.

                                                                                           v²

2. Нормальное ускорение: а_п = —.

                                                                                           r

 Скорость на второй секунде будет равна v 2 = 5 ∙ 2+1,2 = 11,2 м/с.

  (11,2)²

 Величина нормального ускорения: аn2 = ——— = 12,54 м/с² .

                                                                                                                              10

3. Полное ускорение: а = √ a t²+ an².
Полное ускорение в конце второй секунды:
а₂ = √5² + 12,54² = 13,5 м/с².

4. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.

Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, т. к. касательное ускорение — положительная величина (скорость растет).

Контрольные вопросы и задания

1. Запишите в общем виде закон движения в естественной и ко­ординатной форме.

2. Что называют траекторией движения?

3. Как определяется скорость движения точки при естественном способе задания движения?

4. Запишите формулы для определения касательного, нормаль­ного и полного ускорений.

5. Что характеризует касательное ускорение и как оно напра­влено по отношению к вектору скорости?

6. Что характеризует и как направлено нормальное ускорение?

                     Тема 1.8. Кинематика точки                                        71

             ЛЕКЦИЯ 10

---

Дата добавления: 2019-09-13; просмотров: 1582; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!