Тема 1.5. Пространственная система сил

Знать момент силы относительно оси, свойства момента, аналитический способ определения равнодействующей, условия равновесия пространственной системы сил.

Уметь выполнять разложение силы на три взаимно перпенди­кулярные оси, определять момент силы относительно оси.

Пространственная система сил — система сил, линии дей­ствия которых не лежат в одной плоскости.

Момент силы относительно оси

Момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересече­ния оси с плоскостью (рис. 7.1а).

                

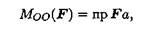
а — расстояние от оси до проекции F ;

np F — проекция силы на плоскость, перпендикулярную оси ОО.

Np F = F cos α; Moo{F) = F cos a ∙ а .

                 

 

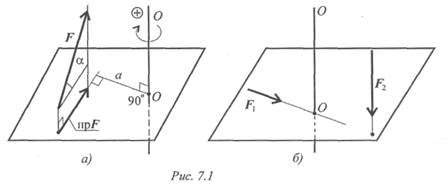
Момент считаем положительным, если сила разворачивает тело по часовой стрелке. Смотреть со стороны положительного направле­ния оси.

                   Тема 1.5. Пространственная система сил                                  51

Если линия действия силы пересекает ось или линия действия силы параллельна оси, моменты силы относительно этой оси равны нулю (рис. 7.16).

Силы и ось лежат в одной плоскости, они не смогут повернуть тело вокруг этой оси.

                                       

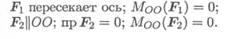
Пространственная сходящаяся система сил

Вектор в пространстве

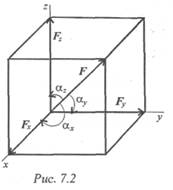
В пространстве вектор силы проецируется на три взаимно пер­пендикулярные оси координат.  Проекции  вектора  образуют  ребра  прямоугольного параллелепипеда, век­тор силы совпадает с диагональю (рис. 7.2).

Модуль вектора может быть полу­чен из зависимости

 

           

 

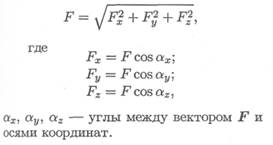
Пространственная сходящаяся система сил

Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересе­каются в одной точке.

Равнодействующую пространственной системы сил можно опре­делить, построив пространственный многоугольник (рис. 7.3),

     

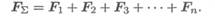
Доказано, что равнодействующая системы сходящихся сил при­ложена в точке пересечения линий действия сил системы.

Модуль равнодействующей пространственной системы сходя­щихся сил можно определить аналитически, использовав метод про­екций.

52                                                                         Лекция 7

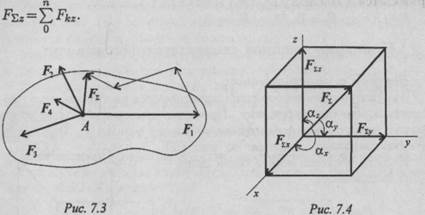
Совмещаем начало координат с точкой пересечения линий дей­ствия сил системы. Проецируем все силы на оси координат и сум­мируем соответствующие проекции (рис. 7.4). Получим проекции равнодействующей на оси координат:                                  

                                      

 

               

 

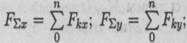
Модуль равнодействующей системы сходящихся сил определим по формуле    

                                     

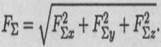
Направление вектора  равнодействующей   определяется   углами

           

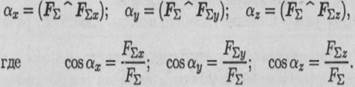
Произвольная пространственная система сил

Приведение произвольной пространственной системы сил к центру О

Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О.

Силы необходимо параллельно перемещать, при этом образует­ся система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения.

                 Тема 1.5. Пространственная система сил                                53

В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) -F_гл (рис. 7.56).

Моменты пар сил можно сложить, получив суммарный момент системы М_гл (главный момент).

Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.

               

 

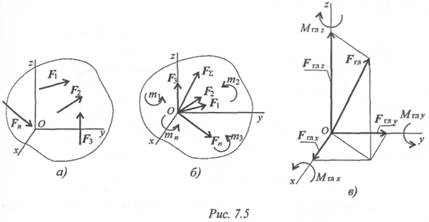
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 7.5в).

Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.

Абсолютное значение главного вектора (рис. 7.56) равно

 

                     

54                                                     Лекция 7

---

Дата добавления: 2019-09-13; просмотров: 1479; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!