Частные случаи приведения системы сил к точке
При приведении системы сил к точке возможны следующие варианты:

Условие равновесия произвольной плоской системы сил
1. При равновесии главный вектор системы равен нулю (Fгл = 0).
Аналитическое определение главного вектора приводит к выводу:

где F kx и F ky — проекции векторов на оси координат.
2. Поскольку точка приведения выбрана произвольно, ясно, что
при равновесии сумма моментов сил системы относительно любой
точки на плоскости должна равняться нулю:
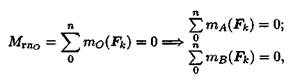
где А и В — разные точки приведения.
38 Лекция 5
Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:
Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.
Получим основную форму уравнения равновесия:

Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно составить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.
Таким образом, имеем пять независимых уравнений равновесия.
Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия.

Тема 1.4. Плоская система произвольно расположенных сил 39

Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
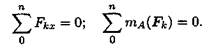
Ось Ох системы координат параллельна линии действия сил.
Примеры решения задач
Пример 1. Найти момент присоединенной пары при переносе силы F 3в точку В (рис. 5.3). F 1 = 10кН; F 2 = 15кН; F3 = 18кН; а = 0,2 м.
Решение
Используем теорему Пуансо. Мв(-Рз) = 18 • 0,2 = 3,6кН-м. 
Пример 2. Найти главный вектор системы (рис. 5.4).
F1 = 10 кН; F 2 = 16 кН; F3 = 12 кН; т = 60кН-м.
Решение
Главный вектор равен геометрической сумме сил:
40 Лекция 5

Пример 3. Найти главный момент системы относительно точки В (использовать данные примера 2).
Решение
Главный момент равен алгебраической сумме моментов сил относительно точки приведения:
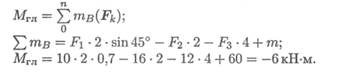
Пример 4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы. F1 = 10kH; F2 = 16kH.
Наносим оси координат и используем уравнения равновесия:
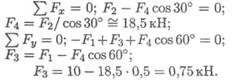

Контрольные вопросы и задания
1. Чему равен главный вектор системы сил?
2. Чему равен главный момент системы сил при приведении ее к точке?
Тема 1.4. Плоская система произвольно расположенных сил 41
3. Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?
Выбрать из предложенных ответов:
— величиной;
— направлением;
— величиной и направлением;
— точкой приложения;
— ничем.
4. Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?
5. Тело вращается вокруг неподвижной оси.
Чему равны главный вектор и главный момент действующей на него системы сил?
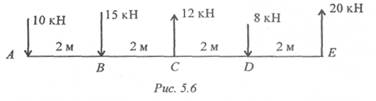
6. Найдите главный вектор и главный момент системы сил, если центр приведения находится в точке А (рис. 5.6).
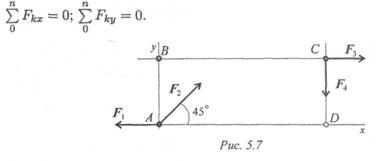
7. Какое еще уравнение равновесия нужно составить, чтобы убедиться в том, что система сил (рис. 5.7) находится в равновесии?
42 Лекция 6
ЛЕКЦИЯ 6
Тема 1.4. Балочные системы.
Дата добавления: 2019-09-13; просмотров: 671; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
