Плоская система сходящихся сил

     Система сил, линии действия которых пе­ресекаются в одной точке, называется сходя­щейся (рис. 2.1).

                                                    

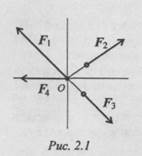
        Необходимо определить равнодействую­щую системы сходящихся сил (F 1 ; F 2 ;F 3 ;. .. ...; F_n), n — число сил, входящих в систему.

       По следствию из аксиом статики, все си­лы системы можно переместить вдоль линии действия, и все силы окажутся приложенными  в одной точке.

       Равнодействующая сходящихся сил

       Равнодействующую двух пересекающихся сил можно опреде­лить с помощью параллелограмма или треугольника сил (4-я ак­сиома) (рис. 2.2).

                  

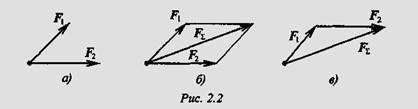
            Используя свойства векторной суммы сил, можно получить равнодействующую любой    сходящейся    системы    сил ,    складывая    последо-

 

 

                   

                   Тема 1.2. Плоская система сходящихся сил                                    13

вательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.

                         

                      

При графическом способе определения равнодействующей век­торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.

Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствую­щим векторам сил.

Порядок построения многоугольника сил

1. Вычертить векторы сил заданной системы в некотором мас­штабе один за другим так, чтобы конец предыдущего вектора со­впадал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоуголь­нике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил

При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если   плоская система    сходящихся  сил  находится  в  равновесии ,

 

 

14                                                    Лекция 2

многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Сравните два треугольника сил (рис. 2.4) и сделайте вывод о количестве сил, входящих в каждую систему.

Рекомендация. Обратить внимание на направление векторов.      

 

                          

Решение задач на равновесие геометрическим способом

Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).

Порядок решения задач:

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу кон­тура.)

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зави­симостей.

Пример 1. Груз подвешен на стержнях и находится в равнове­сии. Определить усилия в стержнях (рис. 2.5а).

                                                          Решение

1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5а).

                                                   Тема 1.2. Плоская система сходящихся сил                                              15

Определяем возможные направления реакций связей «жесткие стержни».

               

Усилия направлены вдоль стержней.

2. Освободим точку А от связей, заменив действие связей их
реакциями (рис. 2.56).

   3. Система находится в равновесии. Построим треугольник сил.
  Построение начнем  с  известной  силы,  вычертив  вектор  F  в  не­ котором масштабе.

Из концов вектора  Fпроводим  линии, параллельные  реакциям  R 1 и R ₂.

Пересекаясь, линии создадут треугольник (рис. 2.5в). Зная мас­штаб построений и измерив длину сторон треугольника, можно опре­делить величину реакций в стержнях.

4. Для более точных расчетов можно воспользоваться геометри-­
ческими соотношениями, в частности теоремой синусов: отношение
стороны треугольника к синусу противоположного угла — величина постоянная

               

                        

      

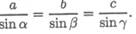
        Для данного случая:

            

16                                                                        Лекция 2

                   

Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.

Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6а).

Решение

             

1. Нанесем на схему возможные направления усилий, приложенных в точке А. Реакции стержней — вдоль стержней, усилие от
каната — вдоль каната от точки А к точке В.

2. Груз находится в равновесии, следовательно, в равновесии
находится точка А, в которой пересекаются три силы.

Освободим точку А от связей и рассмотрим ее равновесие (рис. 2.66).

Замечание. Рассмотрим только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: Тз = 45 кН.

3. Строим треугольник для сил, приложенных в точке А, начиная с известной силы Тз. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке А.

Образовался прямоугольный треугольник (рис. 2.6в).

                 Тема 1.2. Плоская система сходящихся сил                                      17

4. Неизвестные реакции стержней можно определить из соотно­шений в прямоугольном треугольнике:

              

 

Замечание. При равновесии векторы сил в треуголь­нике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 1.26а. Направления совпали, следовательно, направления реакций определены верно.

Контрольные вопросы и задания

1. По изображенным многоугольникам сил (рис. 2.7) решите,
сколько сил входит в каждую систему и какая из них уравновешена.
(Обратить внимание на направление векторов.)

 

         

 

2. Из представленных силовых треугольников выберете тре-­
угольник, построенный для точки А (рис. 2.8, 2.9).

            

        

Шар подвешен на нити и находится в равновесии. Обратить внимание на направление реакции от гладкой опоры и условие рав­новесия шара (рис. 2.8).

18                                                                      Лекция 2                                                                        

 

                             

 

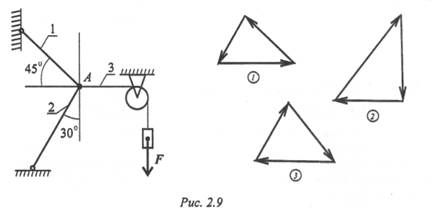
Груз F подвешен на канате и находится в равновесии. Обра­тить внимание на реакции, приложенные к точке А. Силы, не при­ложенные к точке А, не рассматриваются. Не забывать об условии равновесия системы сил (рис. 2.9).

                                                 Тема 1.2. Плоская система сходящихся сил                                                   19

ЛЕКЦИЯ 3

---

Дата добавления: 2019-09-13; просмотров: 783; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!