Определение реакций опор и моментов

Защемления

Иметь представление о видах опор и возникающих реакциях в опорах.

Знать три формы уравнений равновесия и уметь их использовать для определения реакций в опорах балочных систем.

Уметь выполнять проверку правильности решения.

Виды нагрузок и разновидности опор

Виды нагрузок

По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.

Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.

В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).

q — интенсивность нагрузки; l — длина стержня;

G = ql — равнодействующая распределенной нагрузки.

Разновидности опор балочных систем (см. лекцию 1) Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.

Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)

Тема 1.4. Балочные системы 43

Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы Ra _x и Ra _v и парой с моментом M r . Для определения этих неизвестных удобно использовать систему уравнений в виде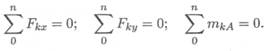

Каждое уравнение имеет одну неизвестную величину и решается без подстановок.

Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например В:

Шарнирно-подвижная опора (рис. 6.3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

Шарнирно-неподвижная опора (рис. 6.4)

Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.

Балка на двух шарнирных опорах (рис. 6.5)

Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему

44 Лекция 6

уравнений во второй форме:

Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.

Из уравнения Σ F kx = 0 определяется реакция R b x .

Из уравнения Σ mkA (Fk) = 0 определяется реакция R b _{у .}

Из уравнения Σ mkB (Fk ) = 0 определяется реакция R а y _.

Для контроля правильности решения используется дополнительное уравнение

При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):

Примеры решения задач

Пример 1. Одноопорная (защемленная) балка нагружена сосредоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.

Тема 1.4. Балочные системы 45

Решение

1. В заделке может возникнуть реакция, представляемая двумя
составляющими (Ra _v ;Ra x ), и реактивный момент МА. Наносим на схему балки возможные направления реакций.

Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.

В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.

2. Используем систему уравнений:

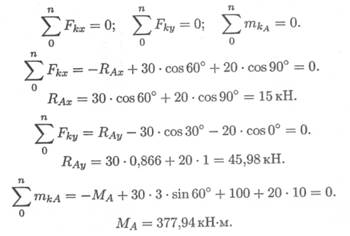
46 Лекция 6

Знаки полученных реакций (+), следовательно, направления реакций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Подставляем значения полученных реакций:

-377,94 + 45,98 • 10 - 210 • 0,866 + 100 = 0;

-559,8 + 559,8 = 0.

Решение выполнено верно.

Пример 2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F , распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 6.8а). Определить реакции опор.

Решение

1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.

Тема 1.4. Балочные системы 47

Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.

2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно.

3. Заменяем распределенную нагрузку сосредоточенной:

Сосредоточенную силу помещаем в середине пролета, далее задача решается с сосредоточенными силами (рис. 6.86).

4. Наносим возможные реакции в опорах (направление произвольное).

5. Для решения выбираем уравнение равновесия в виде

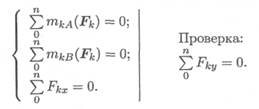
6. Составляем уравнения моментов относительно точек крепления:

Реакция направлена верно.

Реакция отрицательная, следовательно, RA y нужно направить в противоположную сторону.

48 Лекция 6

7. Используя уравнение проекций, получим:

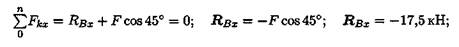
Rb x — горизонтальная реакция в опоре В.

Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.

8. Проверка правильности решения. Для этого используем четвертое уравнение

равновесия Σ F ky ⁼ 0:

- R_Ay - G + R_By - F cos 45° = 0.

Подставим полученные значения реакций.

Если условие выполнено, решение верно:

-5,1 - 12 + 34,6 - 25 · 0,7 = 0.

Контрольные вопросы и задания

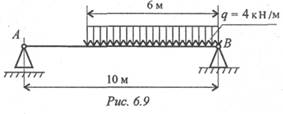
1. Замените распределенную нагрузку сосредоточенной и определите расстояние от точки приложения равнодействующей до опоры А (рис. 6.9).

2. Рассчитайте величину суммарного момента сил системы относительно точки А (рис. 6.10).

Тема 1.4. Балочные системы 49

3. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке?

4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

5. Определите реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).

6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.

50 Лекция 7

ЛЕКЦИЯ 7

Дата добавления: 2019-09-13; просмотров: 3618; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!