Рекомендуем решить самостоятельно задачи № 1 – 3.
Задача 2. Найти величину и направление градиента функции u = 3x2 – 5y + 4z2 + xy в точке М0 (1, 0, -1).
Решение. Как следует из равенства (5.2), координаты вектора 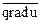 есть частные производные функции u в точке М0, найдем их:
есть частные производные функции u в точке М0, найдем их:
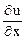 = (6х + у)
= (6х + у) 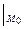 = 6 + 0 = 6,
= 6 + 0 = 6,
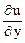 = (-5 + x)
= (-5 + x) 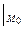 = -5 + 1 = -4,
= -5 + 1 = -4,
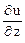 = 12 z2
= 12 z2 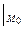 = 12 × 1 = 12.
= 12 × 1 = 12.
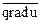 = 6
= 6 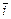 - 4
- 4 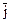 + 12
+ 12 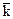 .
.
Величина градиента равна:
| 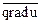 | =
| = 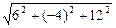 =
= 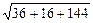 =
= 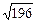 = 14.
= 14.
Найти направление вектора – значит найти его направляющие косинусы. Для вектора градиента будем иметь:
cos a = 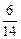 =
= 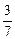 ; cos b =
; cos b = 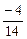 = -
= - 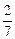 ; cos g =
; cos g = 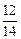 =
= 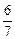 .
.
Задача 3. Написать уравнения касательной плоскости и нормали к поверхности 3 xyz – z3 =8 в точке М0 (0, 2, -2).
Решение. Поверхность задана уравнением F (x, y, z) = 0.
F (x, y, z) = 3xyz – z3 – 8. Поэтому уравнения касательной плоскости и нормали в точке М0 (x0, y0, z0) имеют вид (5.5 ) и (5.1.6).
Найдем частные производные функции F (x, y, z) в точке М0:
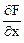 = 3yz
= 3yz 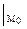 = -12;
= -12;  = 3 xz
= 3 xz 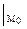 = 0;
= 0; 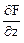 = 3xy – 3z2
= 3xy – 3z2 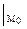 = -12.
= -12.
Запишем уравнение касательной плоскости:
-12 (х – 0) + 0 (у – 2) – 12 (z + 2) = 0 или
-12 х – 12 z - 24 = 0, т.е. x + z + 2 = 0.
Запишем уравнение нормали:
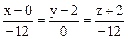 или
или 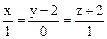 .
.
Задача 4. Написать уравнения касательной плоскости и нормали к поверхности z = 2x2 + 4y2 в точке М0 (2, 1, 12).
Решение. Поверхность задана в явном виде z = f (x, y), поэтому уравнения касательной плоскости и нормали в точке М0 (x0, y0, z0) имеют вид (5.3) и (5.4).
Найдем частные производные функции в точке М0
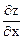 = 4х
= 4х 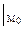 = 8;
= 8; 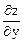 = 8y
= 8y 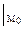 = 8.
= 8.
Уравнение касательной плоскости:
z – 12 = 8 (x – 2) + 8 (y – 1) или
|
|
|
8х + 8у – z – 16 – 8 + 12 = 0
8x + 8y – z – 12 = 0.
Уравнение нормали:
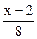 =
= 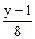 =
= 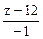 .
.
Задача 5. К поверхности x2 + 2y2 + 3z2 = 21 провести касательные плоскости, параллельные плоскости
х + 4у + 6z = 0.
Решение. Дана плоскость х + 4у + 6z = 0, ее нормальный вектор 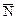 (1, 4, 6). Из условия параллельности плоскостей имеем, что нормальный вектор
(1, 4, 6). Из условия параллельности плоскостей имеем, что нормальный вектор 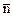 искомых плоскостей коллинеарен данному вектору
искомых плоскостей коллинеарен данному вектору 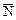 и равен
и равен 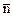 (t, 4t, 6t). Найдем на поверхности точки, в которых нужно провести касательные плоскости.
(t, 4t, 6t). Найдем на поверхности точки, в которых нужно провести касательные плоскости.
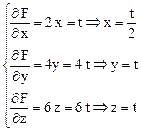 Þ
Þ
подставим в уравнение поверхности x2 + 2y2 + 3z2 = 21 и найдем значение параметра t:
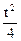 + 2 t2 + 3 t2 = 21,
+ 2 t2 + 3 t2 = 21, 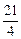 t2 = 21, t2 = 4, t = ± 2.
t2 = 21, t2 = 4, t = ± 2.
Получаем две точки на поверхности: М1 (1, 2, 2) и
М2 (-1,-2,-2). В точке М1 (1, 2, 2): 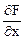 = 2,
= 2, 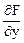 = 8,
= 8, 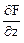 = 12,
= 12,
и уравнение касательной плоскости запишется так:
2 (x – 1) + 8 (y – 2) + 12 (z – 2) = 0,
2x + 8y + 12z – 42 = 0,
x + 4y + 6z – 21 = 0.
В точке М2 (-1,-2,-2): 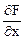 = -2,
= -2, 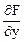 = -8,
= -8, 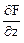 = -12.
= -12.
Запишем уравнение касательной плоскости:
-2 (x + 1) - 8 (y + 2) - 12 (z + 2) = 0,
-2x - 8y - 12z – 42 = 0,
x + 4y + 6z + 21 = 0.
Для закрепления данной темы рекомендуем решить задачи № 11 – 17.
Банк задач для самостоятельной работы
Задача 1. Найти 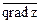 в точке (2, 1), если
в точке (2, 1), если
z = x3 + y3 – 3xy.
Ответ. 9 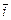 - 3
- 3 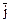 .
.
Задача 2. Найти 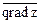 в точке (5, 3), если z =
в точке (5, 3), если z = 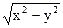 .
.
Ответ. 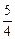
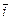 -
- 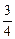
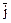 .
.
Задача 3. Найти 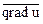 в точке (1, 2, 3), если u = xyz.
в точке (1, 2, 3), если u = xyz.
|
|
|
Ответ. 6 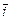 + 3
+ 3 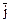 + 2
+ 2 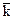 .
.
Задача 4. Найти величину и направление 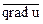 в точке (2, -2, 1), если u = x2 + y2 + z2.
в точке (2, -2, 1), если u = x2 + y2 + z2.
Ответ. | 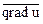 | = 6, cos a =
| = 6, cos a = 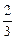 , cos b = -
, cos b = - 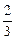 , cos g =
, cos g = 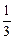 .
.
Задача 5. Найти величину наибольшего подъема поверхности z = x2 + 4 y2 в точке (2, 1, 8).
Ответ. tg j = 4 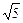 .
.
Задача 6. Найти наибольшую крутизну подъема поверхности z = ln (x2 + 4y2) в точке (6, 4, ln 100).
Ответ. tg j » 0,34.
Задача 7. Найти производную функции z = x2 – xy – 2y2 в точке Р (1, 2) в направлении, составляющем с осью ОХ угол в 60°. Ответ. - 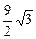 .
.
Задача 8. Найти производную функции
z = x3 – 3x2 y + 3x y2 + 1 в точке (3, 1) в направлении, идущем от этой точки к точке (6, 5). Пояснить ответ.
Ответ. 0.
Задача 9. Найти производную функции z = x2 + 4 y2 в точке (2, 1) в направлении градиента. Сделать чертеж к задаче.
Ответ. 4 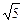 .
.
Задача 10. Найти производную функции z = ln (x + y) в точке (1, 2), принадлежащей параболе у2 = 4х, по направлению этой параболы.
Ответ. 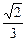 .
.
Задача 11. Найти производную функции u = x2 y2 z2 в точке А (1, -1, 3) в направлении, идущем от этой точки к точке В (0, 1, 1).
Ответ. –22.
Задача 12. Написать уравнение касательной плоскости и уравнение нормали и параболоиду вращения z = x2 + y2 в точке (1, -2, 5). Сделать чертеж.
Ответ. 2x – 4y – z – 5 = 0,
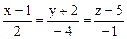 .
.
В задачах 13 – 15 для данных поверхностей найти уравнения касательных плоскостей и нормалей в указанных точках.
|
|
|
13. z = 2x2 – 4y2 в точке (2, 1, 4).
Ответ. 8x – 8y – z – 4 = 0,
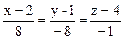 .
.
14. z = 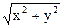 - xy в точке (3, 4, -7).
- xy в точке (3, 4, -7).
Ответ. 17x + 11y + 5z – 60 = 0,
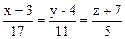 .
.
15. x3 + y3 + z3 + xyz – 6 = 0 в точке (1, 2, -1).
Ответ. x + 11y + 5z – 18 = 0,
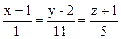 .
.
Задача 16. Показать, что поверхности
x + 2y – ln z + 4 = 0 и x2 – xy – 8x + z + 5 = 0
касаются друг друга (т.е. имеют общую касательную плоскость) в точке (2, -3, 1).
Задача 17. К эллипсоиду x2 + 2y2 + z2 = 1 провести касательную плоскость, параллельную плоскости x – y + 2z = 0.
Ответ. x – y + 2z ± 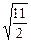 = 0.
= 0.
Варианты проверочной работы
Дано: функция z = f (x, y), точка А (x0, y0) и точка В. Требуется найти: 1) 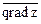 в точке А; 2) производную функции в точке А в направлении, идущем от этой точки к точке В; 3) уравнения касательной плоскости и нормали в точке А.
в точке А; 2) производную функции в точке А в направлении, идущем от этой точки к точке В; 3) уравнения касательной плоскости и нормали в точке А.
1) z = 2x2 + xy A (-1, 2); B (2, 6).
2) z = x2 + xy + y2 A (1, 1); B (3, 0).
3) z = ln (x2 + xy2) A (1, 2); B (4, -2).
4) z = arctg (xy) A (2, 3); B (6, 6).
5) z = x3y + xy2 A (1, 3); B (-4, 15).
6) z = x2y + xy2 A (1, 1); B (7, -7).
7) z = 3x4 + 2x2y3 A (-1, 2); B (3, -1).
8) z = ln (2x + 3y) A (2, 2); B (-1, 4).
|
|
|
9) z = ln (3x2 + 4y2) A (1, 3); B (3, 2).
10) z = ln (5x2 + 4y2) A (1, 1); B (3, 0).
Ответы для второго задания:
1) -2; 2) 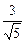 ; 3)
; 3) 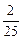 ; 4)
; 4) 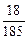 ; 5) -
; 5) - 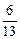 ; 6) -
; 6) - 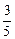 ; 7) -
; 7) - 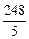 ;
;
8) 0; 9) - 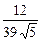 ; 10)
; 10) 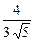 .
.
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Геометрическим изображением функции двух переменных
z = f (x, y) (6.1)
в прямоугольной системе координат является некоторая поверхность. Уравнение (6.1) может быть представлено в виде: F (x, y, z) = 0. Если это уравнение является уравнением второй степени, то поверхность, которую оно представляет, называется поверхностью второго порядка. Рассмотрим некоторые из них.
Цилиндрическая поверхность
Пусть L – некоторая линия в пространстве (назовем ее направляющей). Если через каждую точку этой линии провести прямую, параллельную некоторой прямой l (назовем ее образующей), получим цилиндрическую поверхность.
Уравнение цилиндрической поверхности, направляющая которой лежит в плоскости ХОУ, а образующая параллельна оси OZ, имеет вид: F (x, y) = 0. Эта поверхность изображена на рис. 1.
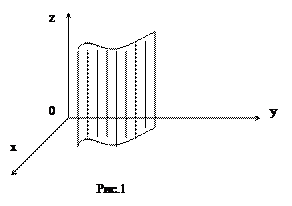 |
Аналогично уравнения F (x, z) = 0 и F (у, z) = 0 определяют цилиндрические поверхности с образующими, параллельными осям ОУ и ОХ соответственно.
Примеры канонических уравнений цилиндров второго порядка:
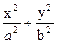 = 1 - эллиптический цилиндр (направляющая –
= 1 - эллиптический цилиндр (направляющая –
эллипс с полуосями а и b, образующая параллельна оси OZ) (рис. 2).
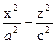 = 1 - гиперболический цилиндр (направляющая –
= 1 - гиперболический цилиндр (направляющая –
гипербола, образующая параллельна оси ОУ)
(рис. 3).
у2 = 2 p z - параболический цилиндр (направляющая –
парабола, образующая параллельна оси ОХ)
(рис. 4).
 |
Рис. 2

Рис. 3
 | |||
| |||
Рис. 4
Эллипсоид
Каноническое уравнение трехосного эллипсоида имеет вид:
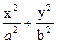 +
+ 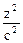 = 1.
= 1.
Чтобы изобразить эту поверхность на чертеже, применим “метод сечений”. Линия пересечения эллипсоида с плоскостью ХОУ определяется системой уравнений:
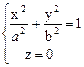
Отсюда видно, что плоскость ХОУ пересекает эллипсоид по эллипсу с полуосями а и b (рис. 2). Аналогичная картина получается при пересечении эллипсоида с координатными плоскостями ХОZ и УОZ. Линии пересечения – эллипсы с полуосями а, c и b, с соответственно (рис. 2).
 |
Рис. 2
Величины a, b, c называются полуосями эллипсоида. Если а = b = c = R, эллипсоид превращается в сферу:
x2 + y2 + z2 = R2.
Однополостный гиперболоид
Каноническое уравнение: 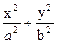 -
- 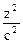 = 1.
= 1.
Наименование “гиперболоид” происходит от того, что среди сечений этой поверхности есть гиперболы. Например, линия пересечения однополостного гиперболоида с плоскостью УОZ (рис. 3) задается системой уравнений - это гипербола с мнимой осью OZ:
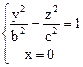 (1)
(1)

Рис. 3
Любая плоскость, параллельная плоскости ХОУ, пересекает гиперболоид по эллипсу (рис. 3):
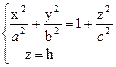 (2)
(2)
в частности,
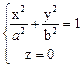 (3)
(3)
Двуполостный гиперболоид
Поверхность, представляемая уравнением
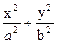 -
- 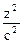 = -1,
= -1,
называется двуполостным гиперболоидом. Она состоит из двух обособленных полостей. Действительно, ни одна из плоскостей ХОУ не пересечет поверхности при | z | < c, т.к. при этом система
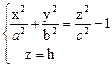
не имеет решений. При z = + c в сечении – точки, которые называются вершинами двуполостного гиперболоида. При
| z | > c в сечении эллипсы. Размеры их увеличиваются по мере возрастания z (рис. 4)
Рис. 4
Сечения плоскостями XOZ и УOZ, которые представлены системами
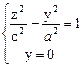
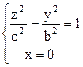 ,
,
являются гиперболами с действительной осью OZ.
Конус второго порядка
Поверхность, представляемая уравнением
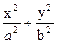 -
- 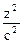 = 0, называется конусом второго порядка.
= 0, называется конусом второго порядка.
|
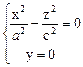 , которая представляет пару прямых
, которая представляет пару прямых 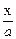 +
+ 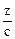 = 0
= 0 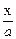 -
- 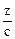 = 0, проходящих через начало координат (рис. 5).
= 0, проходящих через начало координат (рис. 5).

Рис. 5
Всякая плоскость, параллельная плоскости ХОУ (но не совпадающая с ней), пересекает конус по эллипсу:
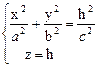 .
.
Эллиптический параболоид
Эллиптический параболоид – это поверхность, представляемая уравнением:
z = 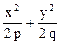 (р > 0, q > 0)
(р > 0, q > 0)
Сечения поверхности плоскостями ХОZ и УОZ – это параболы х2 = 2 р z (y = 0) и y2 = 2 q z (x = 0) (рис. 6). Сечения плоскостями, параллельными плоскости ХОУ, задаются системой:
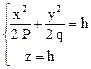 ,
,
которая не имеет решения при h < 0.
При h = 0 плоскость z = 0 имеет с поверхностью одну общую точку. При h > 0 сечение представляет собой эллипс, размеры которого возрастают с увеличением h (рис. 6).
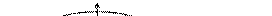
Рис. 6.
Гиперболический параболоид
Гиперболический параболоид – это поверхность, представляемая уравнением:
z = 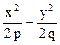 (р > 0, q > 0).
(р > 0, q > 0).
Сечения плоскостями XOZ и УОZ есть параболы:
(1) x2 = 2 p z (y = 0)
(2) y2 = -2 q z (x = 0)

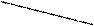 Ветви параболы (1) направлены вверх, параболы (2) – вниз. ( Рис. 7). В результате поверхность имеет седлообразный вид.
Ветви параболы (1) направлены вверх, параболы (2) – вниз. ( Рис. 7). В результате поверхность имеет седлообразный вид.
 | |||
| |||
Рис. 7
Всякая плоскость, параллельная плоскости ХОУ (но не совпадающая с ней), пересекает поверхность по гиперболе:
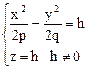 .
.
При z = 0 линия пересечения – пара прямых: 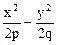 = 0, т.е.
= 0, т.е.
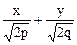 = 0 и
= 0 и 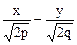 = 0.
= 0.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1975, гл. 10: Функции нескольких переменных. Дифференциальное исчисление. – С. 185 – 201, гл. II: Применения дифференциального исчисления функций нескольких переменных. – С. 202 – 216.
2. Задачи и упражнения по математическому анализу. Для втузов / Бараненков Г.С., Демидович Б.П., Ефименко В.А. и др. – М.: Наука, 1968, гл. 6: Функции нескольких переменных. – С. 172 – 232.
3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1962, гл. 6: Дифференциальное исчисление функций нескольких переменных. –
С. 288 – 344.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, 1970 – 1985. Т. 1, гл. УIII. Функции нескольких переменных. – С. 243 – 304.
Дата добавления: 2019-09-13; просмотров: 2529; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
