В чем заключается механический смысл
Частных производных ?
Механический смысл частных производных следует из их определения.
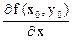 - скорость изменения функции в точке М0 (x0, y0) в
- скорость изменения функции в точке М0 (x0, y0) в
направлении оси ОХ.
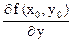 - скорость изменения функции в точке М0 (x0, y0) в
- скорость изменения функции в точке М0 (x0, y0) в
направлении оси ОУ.
2.1.4. Когда функция z = f (x, y) называется
Дифференцируемой в данной точке ?
Определение. Функция z = f (x, y) называется дифференцируемой в точке М0 (x0, y0), если в этой точке полное приращение функции можно представить в виде:
D z = A D x + B D y + O (r),
где А и В – числа, r = 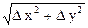 , O (r) – бесконечно малая высшего порядка относительно r при D х ® 0, D y ® 0.
, O (r) – бесконечно малая высшего порядка относительно r при D х ® 0, D y ® 0.
Что называется полным дифференциалом
Функции двух переменных ?
Определение. Полным дифференциалом функции
z = f (x, y) называется главная часть полного приращения Dz, линейная относительно приращений аргументов D х и Dy, т.е. dz = A Dх + В Dy.
Дифференциалы независимых переменных совпадают с их приращениями, т.е. dx = Dх и dy = Dy. Полный дифференциал вычисляется по формуле:
dz = 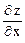 dx +
dx + 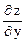 dy.
dy.
Вывести формулу применения полного
Дифференциала к вычислению приближенного
Значения функции в точке
При достаточно малом r = 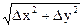 Dz » dz, т.е.
Dz » dz, т.е.
Þ f (x0 + D x, y0 + D y) – f (x0, y0) = dz (x0, y0), откуда
f (x0 + D x, y0 + D y) = f (x0, y0) +  Dx +
Dx + 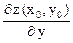 Dy
Dy
(2.1.1)
Примеры решения задач
|
|
|
Задача 1. Найти частные производные функции двух переменных
z = ln cos 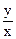 .
.
Решение. Дифференцируем функцию по х, рассматривая у как постоянную величину, получим:
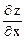 =
= 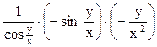 .
.
Аналогично, считая x постоянной величиной, найдем
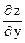 =
= 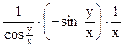 .
.
Задача 2. Найти частные производные функции трех переменных
U = 2x + 3y – 4z + x4 y3 z2.
Решение .
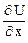 = 2 + 4x3 y3 z2;
= 2 + 4x3 y3 z2; 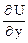 = 3 + 3x4 y2 z2;
= 3 + 3x4 y2 z2;
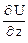 = -4 + 2x4 y3 z.
= -4 + 2x4 y3 z.
Задача 3. Под каким углом пересекаются плоские линии, получающиеся в результате пересечения поверхностей
z = x2 + 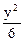 и z =
и z = 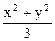 плоскостью у = 2 ?
плоскостью у = 2 ?
Решение. В результате пересечения эллиптического параболоида z = x2 + 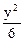 плоскостью у = 2 получим параболу
плоскостью у = 2 получим параболу
z = x2 + 2/3, а параболоида вращения z = 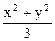 - параболу
- параболу
z = 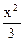 +
+ 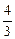 . Найдем точку пересечения этих парабол:
. Найдем точку пересечения этих парабол:
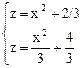 Þ х2 + 2/3 =
Þ х2 + 2/3 = 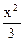 +
+ 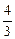 ;
;
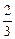 x2 = 2/3; x2 = 1; x = ± 1.
x2 = 2/3; x2 = 1; x = ± 1.
Нарисуем параболы в плоскости ХОZ
 |
Рассмотрим точку А (1, 2, 5/3). Углом между двумя кривыми называется угол между касательными к этим кривым в точке их пересечения. Используя геометрический смысл частных производных, мы найдем угловые коэффициенты касательных в точке А, а именно:
z1 = x2 + y2/6; k1 = 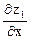 = 2 x ½x =1 = 2
= 2 x ½x =1 = 2
z2 = 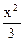 +
+ 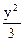 ; k2 =
; k2 = 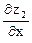 =
= 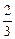 x ½x =1 =
x ½x =1 = 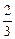 .
.
Найдем тангенс угла между двумя прямыми по формуле:
|
|
|
tg a = 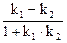
tg a = 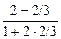 =
= 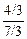 =
= 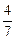
a = arctg 4/7.
Задача 4. Для функции z = f (x, y) = x2 + y найти полное приращение и полный дифференциал в точке (2, 1); сравнить их, если Dх = -0,1; Dy = 0,2.
Решение. Найдем полное приращение функции Dz:
Dz:= f (x + Dх,y + Dy)– f (x, y) = [(x + Dх)2 + (y + Dy)]– (x2 + y) =
= x2 + 2x × Dх + Dх2 + y + Dy - x2 - y = 2x × Dх + Dy + Dх2.
Линейная относительно Dх, Dy часть приращения функции называется полным дифференциалом и обозначается dz, т.е.
dz = 2x × Dх + Dy.
Найдем численное значение Dz и dz согласно условию задачи.
Dz:= 2x × Dх + Dy + Dх2 = 2 × 2 (-0,1) + 0,2 + (-0,1)2 =
= - 0,4 + 0,2 + 0,01 = -0,19,
dz = 2x × Dх + Dy = 2 × 2 (-0,1) + 0,2 = -0,4 + 0,2 = -0,2.
С точностью до бесконечно малых высшего порядка можно написать приближенное равенство: Dz » dz, которое используется в приближенных вычислениях.
Задача 5. Найти полный дифференциал функции
z = sin x2 × ay.
Решение. Вычислительная формула полного дифференциала имеет вид:
dz = 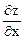 dx +
dx + 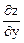 dy.
dy.
Найдем частные производные данной функции
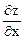 = cos x2 × 2x × ay,
= cos x2 × 2x × ay, 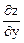 = sin x2× ay ln a.
= sin x2× ay ln a.
Полный дифференциал равен:
dz = (cos x2 × 2x × ay) dx + (sin x2× ay ln a) dy.
Задача 6. Вычислить приближенно 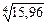 +
+ 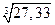 .
.
Решение. Используем формулу приближенного вычисления (2.1.6):
f (x0 + Dx, y0 + Dy) » f (x0, y0) + 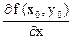 Dx +
Dx + 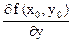 Dy.
Dy.
Запишем наше выражение в виде функции
|
|
|
f (x, y) = 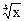 +
+ 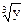 ,
,
где х = 15,96, y = 27,03.
Выберем за х0, у0 числа близкие к х и у.
Пусть х0 = 16, y0 = 27. Найдем приращения аргументов:
Dx = х - х0, Dx = 15,96 –16 = -0,04,
Dy = у – у0, Dy = 27,08 – 27 = 0,08.
Найдем частные производные в точке (х0; у0) = (16; 27).
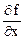 =
= 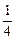
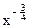 =
= 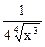 ;
;
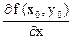 =
= 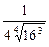 =
= 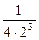 =
= 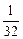 = 0,03
= 0,03
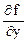 =
= 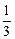
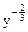 =
= 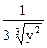 ;
;
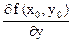 =
= 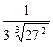 =
= 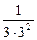 =
= 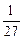 = 0,037.
= 0,037.
Найдем f (x0, y0) = 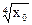 +
+ 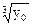 =
= 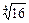 +
+ 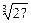 = 2 + 3 = 5..
= 2 + 3 = 5..
Подставляя найденные значения в формулу приближенных вычислений, получим:
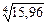 +
+ 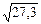 » 5 +0,03 × (-0,04) + 0,037 × 0,03 =
» 5 +0,03 × (-0,04) + 0,037 × 0,03 =
= 5 – 0,0012 + 0,00111 = 5 – 0,00009 = 4,99991.
Дата добавления: 2019-09-13; просмотров: 201; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
