Как определяются частные производные
Высших порядков ?
Производные второго порядка можно снова дифференцировать по х и у. Получим частные производные 3го порядка. Их будет, очевидно, уже восемь: 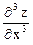 ,
, 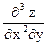 ,
, 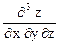 ,
,
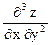 ,
, 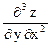 ,
, 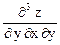 ,
, 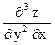 ,
, 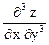 .
.
Определение. Частная производная n-го порядка от функции z = f (x, y) есть производная от производной (n–1)-го порядка.
Например: 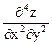 =
= 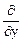
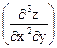 .
.
Для функции любого числа переменных частные производные высших порядков определяются аналогично.
Что называют дифференциалом второго
Порядка функции двух переменных ?
Определение. Дифференциалом второго порядка функции z = f (x, y) называется дифференциал от ее дифференциала первого порядка и обозначается:
d2 f (x, y) = d (d f (x, y))
Если функция z = f (x, y) имеет непрерывные частные производные второго порядка, то вычислительная формула для d2 f (x, y) имеет вид:
d2 f (x, y) = 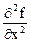 dx2 + 2
dx2 + 2 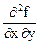 dx dy +
dx dy + 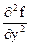 dy2
dy2
Примеры решения задач
Задача 1. Найти полную производную 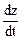 функции
функции
z = ln (x2 + y2), если х = 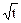 , y = t2 + 1.
, y = t2 + 1.
Решение. Используем правило дифференцирования сложной функции (3.1.1):
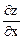 =
= 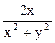 ;
; 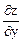 =
= 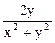 ;
; 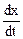 =
= 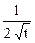 ;
; 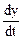 = 2 t.
= 2 t.
Окончательно получаем:
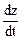 =
= 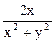 ×
× 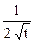 +
+ 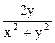 × 2 t =
× 2 t = 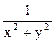
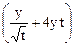 .
.
Задача 2. Найти частную производную 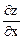 и полную производную
и полную производную 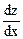 , если z = exy, где у = j (х).
, если z = exy, где у = j (х).
Решение. Частная производная по х равна: 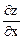 = exy × у. Полную производную найдем по формуле дифференцирования сложной функции (3.12):
= exy × у. Полную производную найдем по формуле дифференцирования сложной функции (3.12):
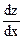 = exy × у + exy × х × j¢(х) = exy (у + х j¢ (х)).
= exy × у + exy × х × j¢(х) = exy (у + х j¢ (х)).
|
|
|
Задача 3. Найти 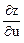 и
и 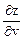 , если z = x + y2, где
, если z = x + y2, где
x = v2 + sin u, y = ln (u2 + v).
Решение. Частные производные 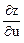 и
и 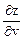 , найдем по формуле дифференцирования сложной функции (3.1.3):
, найдем по формуле дифференцирования сложной функции (3.1.3):
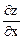 = 1;
= 1; 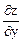 = 2y;
= 2y; 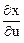 = cos u;
= cos u; 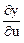 =
= 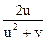 ;
;
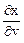 = 2v;
= 2v; 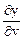 =
= 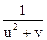 .
.
Окончательно имеем:
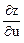 = 1 × сos u + 2y ×
= 1 × сos u + 2y × 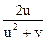 = cos u +
= cos u + 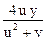
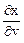 = 1 × 2v + 2y ×
= 1 × 2v + 2y × 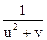 = 2v +
= 2v + 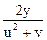 .
.
Самостоятельно рекомендуем решить задачи № 1 – 8.
Задача 4. Найти производную по х функции у, заданной неявно:
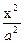 +
+ 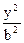 - 1 = 0.
- 1 = 0.
Решение. Неявная функция задана уравнением
F (x, y) = 0. Искомую производную найдем по формуле (3.1.5):
Fx¢ = 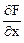 =
= 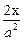 ; Fy¢ =
; Fy¢ = 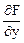 =
= 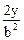 ;
;
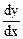 = -
= - 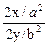 = -
= - 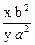 .
.
Задача 5. Найти частные производные функции z, заданной неявно
х2 – 2у2 + 3z2 – y z + y = 0.
Решение. Неявная функция задана уравнением
F (x, y, z) = 0. Искомые частные производные найдем по формуле (3.1.4):
Fx¢ = 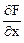 = 2х; Fy¢ =
= 2х; Fy¢ = 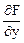 = - 4у – z + 1; Fz¢ =
= - 4у – z + 1; Fz¢ = 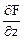 = 6 z – y.
= 6 z – y.
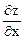 = -
= - 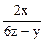 ;
; 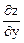 = -
= - 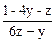 .
.
Задача 6. Найти все частные производные второго порядка функции
z = x3 – 4 x2y + 5 y2.
Решение . Сначала найдем частные производные первого порядка:
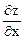 = 3 х2 – 8 ху;
= 3 х2 – 8 ху; 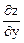 = - 4х2 + 10 у.
= - 4х2 + 10 у.
Мы видим, что 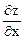 и
и 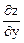 являются функциями двух переменных, значит их можно еще дифференцировать по каждой переменной. Найдем частные производные второго порядка:
являются функциями двух переменных, значит их можно еще дифференцировать по каждой переменной. Найдем частные производные второго порядка:
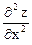 = 6х – 8 у;
= 6х – 8 у; 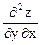 = - 8 х;
= - 8 х;
|
|
|
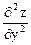 = 10;
= 10; 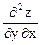 = - 8 х.
= - 8 х.
Еще мы убеждаемся в том, что смешанные производные равны, т.е.
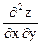 =
= 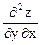 .
.
Задача 7. Найти полные дифференциалы первого и второго порядков функции
z = 2x2 – 3 xy + y3.
Решение. Имеем: 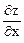 = 4х – 3у;
= 4х – 3у; 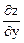 = -3x + 3y2.
= -3x + 3y2.
Поэтому dz = (4x – 3y) dx + (3y2- 3x) dy.
Далее найдем частные производные второго порядка:
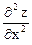 = 4;
= 4; 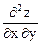 = -3;
= -3; 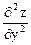 = 6y.
= 6y.
Полный дифференциал второго порядка равен:
d2 z = 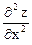 dx2 + 2
dx2 + 2 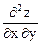 dx dy +
dx dy + 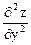 dy2.
dy2.
Для данной функции будем иметь:
d2z = 4 dx2 – 6 dx dy + 6 y dy2.
Для закрепления данной темы предлагаем решить задачи 9 – 24.
Дата добавления: 2019-09-13; просмотров: 176; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
