Банк задач для самостоятельной работы

 

В задачах 1 – 10 найти частные производные функций

 

1. z = x³ + y³ – 3 a xy.

2. z = x³ y – y³ x.

3. z = (5x²y – y³ + 7)³.

4. z = ln (x² + y²).

5. z = x^y.

6. z = (1 + ху)^у

7. u = xy + yz + zx.

8. u = x³ + yz² + 3yx – x + z.

9. u = (sin x)^yz.

10.z = ln     в точке (1, 2)

Ответ.  = 1,  = .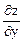

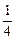Задача 11. Показать, что х ×  + у × 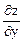 = ху + z, если

z = xy + x × .

Задача 12. Какой угол образует с положительным направлением оси ОХ касательная к линии

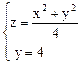в точке (2, 4, 5) ?                     Ответ. 45°.

Задача 13. Какой угол образует с положительным направлением оси ординат касательная к линии

       в точке (1, 1, ) ? Ответ. 30°.

Задача 14. Под каким углом пересекаются плоские линии, получающиеся в результате пересечения поверхностей

z = x² +  y² и     z = 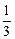 (x² + y²) плоскостью у = 2 ?

                                              Ответ. j = arctg .

Задача 15. Для функции f (x, y) = x + y² найти полное приращение и полный дифференциал в точке (3, 5); сравнить их, если Dх = 0,1; Dy = - 0,3.

                                  Ответ. Dz = -2,81, dz = -2,9.

Задача 16. Для функции f (x, y) = x²y найти полное приращение и полный дифференциал в точке (1, 2); сравнить их, если Dx = 0,1; Dy = 0,2.

                                  Ответ. Dz = 0,662; dz = 0,6.

В задачах 17 – 19 найти полные дифференциалы функций:

17. z = x² y⁴ – x³ y³ + x⁴ y².

18. z = .

19. z = arcsin .

В задачах 20 – 23 вычислить приближенно.

20. sin 1,59 × tg 3,09.                        Ответ. – 0,05.

21. 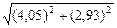.                     Ответ. 4,996.

22. (1,04)^2,02.                                     Ответ. 1,08.

23. ln (  +  - 1).               Ответ. 0,005.

 

Варианты проверочной работы.

 

В задачах 1 – 2 найти частные производные функций, в задачах 3 – 4 найти полные дифференциалы функций.

Вариант 1                                Вариант2

 

1. z = x² y + xy²                            1. z = x + y + 2xy

2. u =                      2. .u =

3. z = x/y                                       3. z = y/x

4. u = x³ – 4x² y + 5z                    4. u = x² – 3xy + yz

 

Вариант 3                                        Вариант4

 

1. z = x² × sin y                              1. z = x³ × tg y

2. u = arctg (x y² z)                        2. u = arccos (x y² z)

3. z = e^y/x                                       3. z =

4. u = ln                                   4. u =

 

Вариант 5                                Вариант 6

 

1. z =                                  1. z =

2. u = ln (x + 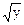 + z)                   2. u = x² ln (y × z)

3. z = cos x × arctg y                      3. z = arcsin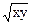

4. u = 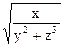                            4. u =

 

Вариант 7                                Вариант 8

 

1. z = x × cos (y²)                           1. z = x³ × cos² y

2. u = 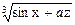                         2. u = x^yz

3. z =                                      3. z = ln

4. u = arctg               4. u =

 

Вариант 9                      Вариант 10

 

1. z = arcsin (x² + y)          1. z = arctg (x + y²)

2. u =                  2. u = (y z)^{sin x}

3. z =  × ln x              3. z = 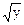 × ln (xy)

4. u =                4. u =

 

 

3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ, НЕЯВНОЙ ФУНКЦИИ, ПОВТОРНОЕ ДИФФЕРЕНЦИРОВАНИЕ

Теоретические сведения

3.1.1. Пусть z = f (x, y), где x = j (t), y = y (t), как    найти производную от сложной функции

z = f [( j (t), y (t)] ?

Если j (t) и y (t) дифференцируемы, то производная от сложной функции вычисляется по формуле:

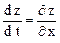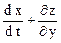 ×  ×             (3.1.1)

 

3.1.2. Пусть z = f (x, y), где y = j (х), как тогда

Вычисляется полная производная по х ?

Производная   вычисляется по формуле:

 +           (3.1.2)

3.1.3. Пусть z = f (x, y), где х = х (u, v), y = y (u, v). Как

     вычислить частные производные   и  ?

 

Частные производные вычисляются по формулам:

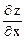
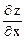
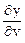 =  +  =  + (3.1.3)

 

Как дифференцируют функции ,заданные

Неявно ?

Ответ на этот вопрос дает теорема о существовании неявной функции.

Теорема. Пусть выполнены условия:

1) F (x, y, z) непрерывна и имеет непрерывные частные производные в точке М₀ (x₀, y₀, z₀) и некоторой ее окрестности.

2) F (x₀, y₀, z₀) = 0.

3)  ¹ 0.

Тогда равенство F (x, y, z) = 0 определяет неявную функцию z = f (x, y), удовлетворяющую условиям 1) z = f (x, y) однозначна и непрерывна в окрестности точки Р₀ (x₀, y₀);

2) z (x₀, y₀ ) = z₀; 3) имеет частные производные, которые вычисляются по формулам:

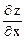 = - ;                = -              (3.1.4)

Формула для вычисления производной неявной функции у = f (x), заданной уравнением F (x, y) = 0 вытекает из формул (3.1.4):

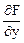 = -   при условии, что (х, y) ¹ 0.                     

 

Что называют частными производными

      второго порядка от функции z = f (x, y) ?

 

Пусть функция z = f (x, y) имеет в области D обе частные производные первого порядка:  и ., которые сами являются функциями х, у. Поэтому от них снова можно находить частные производные.

Определение. Частные производные от 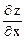 и  называются частными производными второго порядка от функции

z = f (x, y).

Частные производные второго порядка обозначаются так:

 = ;      = ;    

 = ;  = .

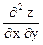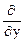
Производные   и  называются смешанными. Для них справедлива теорема: Если функция z = f (x, y) в некоторой окрестности точки М₀ (х₀, y₀) имеет непрерывные вторые частные производные, то  = , т.е. смешанные производные, отличающиеся последовательностью дифференцирования, совпадают.

 

---

Дата добавления: 2019-09-13; просмотров: 148; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!