Банк задач для самостоятельной работы
Задача 1. Найти  , если z = ex-2y, где x = sin t, y = t3.
, если z = ex-2y, где x = sin t, y = t3.
Задача 2. Найти  , если z = arcsin (x – y), где x = 3t,
, если z = arcsin (x – y), где x = 3t,
y = 4t3.
Задача 3. Найти  , если z = x2 + y2 + xy, где x = sin t,
, если z = x2 + y2 + xy, где x = sin t,
y = et.
Задача 4. Найти  , если z = arctg (xy),где y = ex.
, если z = arctg (xy),где y = ex.
Задача 5. u = ln (ex + ey).  = ? Найти
= ? Найти  , если у = х3.
, если у = х3.
Задача 6. Найти 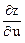 ,
,  , если z = x2y – y2x, где
, если z = x2y – y2x, где
x = u × cos v, y = u × sin v.
Задача 7. Найти 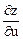 ,
,  , если z = x2 ln y, где x =
, если z = x2 ln y, где x = 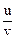 ,
,
y = 3u – 2v.
Задача 8. Показать, что функция z = arctg 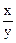 , где
, где
x = u + v, y = u – v удовлетворяет соотношению
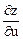 +
+  =
= 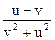 .
.
В задачах 9 – 13 найти производные функций, заданных неявно.
9. х3у – у3х = а4. 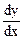 = ? Ответ.
= ? Ответ. 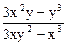 .
.
10. ху – ln y = a. 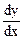 = ? Ответ.
= ? Ответ. 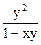 .
.
11. sin (xy) – exy – x2y = 0. 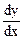 = ?
= ?
Ответ. 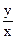 ×
× 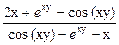 .
.
12. х2 – 2у2 + z2 – 4x + 2z – 5 = 0.  = ?
= ?  = ?
= ?
Ответ.  =
= 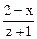 ;
;  =
= 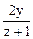 .
.
13. х2 + y2 – z2 – xy = 0. Найти 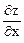 ,
, 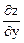 при х = -1,
при х = -1,
y = 0, z = 1 Ответ. –1; 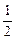 .
.
Задача 14. F (x,y, z) = 0. Доказать, что
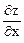 ×
× 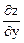 =1;
=1;  ×
× 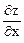 ×
× 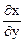 = -1.
= -1.
Задача 15. z =x3 + xy2 – 5 xy3 + y5. Показать, что
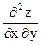 =
= 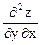 .
.
Задача 16. z = xy. Показать,что 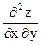 =
= 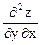 .
.
Задача 17. z = sin (xу). Показать, что
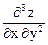 =
= 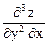 =
= 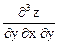 .
.
Задача 18. Найти все частные производные второго порядка
u = 2x +xy + yz.
Ответ.  =
= 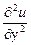 =
=  = 0,
= 0,
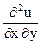 =
= 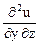 =
= 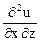 = 1.
= 1.
Задача 19. u = ex (x cos y – y sin y).
Показать, что  +
+ 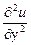 = 0.
= 0.
Задача 20. V = xm yn zp. Найти 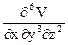 .
.
Ответ. m n p (n – 1) (n – 2) (p – 1) xm - 1 yn - 3 z p – 2,
Задача 21. u = ex y z. Показать, что
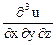 = ху
= ху 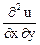 + 2х
+ 2х  + u.
+ u.
В задачах 22 – 23 найти дифференциалы второго порядка.
22. z = xy2 – x2 y.
Ответ. d2 z = 2y dx2 + 4 (y – x) dx dy + 2x dy2.
23. u = y z x.
Ответ. d2 z = 2 (z dx dy + y dx dz + x dy dz).
|
|
|
Задача 24. z = sin (2x + y). Найти d3 z в точке (0, p).
Ответ. (2 dx + dy)3.
Варианты проверочной работы
В первом задании найти 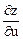 ,
,  ; во втором найти частные производные функции z, заданной неявно, в третьем задании найти частные производные 2-го порядка.
; во втором найти частные производные функции z, заданной неявно, в третьем задании найти частные производные 2-го порядка.
Вариант № 1 Вариант № 2
1. z = 2xy – x, где 1. z = x2 y – y2 x, где
x = u2 + v, y = u + v2 x = u × sin v, y = v cos u
2. x2 + y2 + z2 = a2 2. 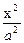 +
+  +
+ 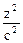 - 1 = 0
- 1 = 0
3. z = x3 – 4 x2y + 5y2 3. z = ln (x + e-y)
Вариант № 3 Вариант № 4
1. z = arctg (x – y), где 1. z = ln sin (x 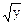 ), где
), где
x = 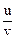 , y = u v x = cos (u-v), y = sin (u-v)
, y = u v x = cos (u-v), y = sin (u-v)
2. (yz)x = (x)yz 2. x – y tg a z = 0
3. z = ey/x 3. z = arctg 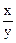
Вариант № 5 Вариант № 6
1. z = tg ln (x y), где 1. z = xy, где
x = u 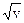 , y =
, y = 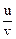 x = sin (u+2v), y = sin (u-v)
x = sin (u+2v), y = sin (u-v)
2. z2 +  -
- 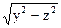 = 0 2. y – x × ctg a z = 0
= 0 2. y – x × ctg a z = 0
3. z = exy 3. z = ex/y
Вариант № 7 Вариант № 8
1. z = e3x-2y, где 1. z = ln 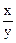 , где
, где
|
|
|
x = tg (uv), y = 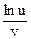 x = u – v2, y = u2 + v
x = u – v2, y = u2 + v
2. x cos y + y cos z + z cos x = 1 2. x2 + y2 – z2 – xy = 0
3. z = 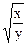 3. z = ln (x2 + y2)
3. z = ln (x2 + y2)
Вариант № 9 Вариант № 10
1. z = arctg 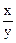 , где 1. z = arcsin
, где 1. z = arcsin 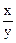 , где
, где
x = 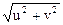 , y =
, y = 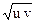 x = u cos v, y = v sin u
x = u cos v, y = v sin u
2. x2 + 2y2 + z2 – 3 x y z – 2y = 0 2.  + ln x = 0
+ ln x = 0
3. z = x × sin (x + y) 3. z = 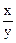 +
+ 
4. ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
Теоретические сведения
Что называют максимумом (минимумом)
функции z = f (x, y) в точке М0 (x0, y0) ?
Пусть функция z = f (x, y)определена в области D и точка М0 (x0, y0) является внутренней точкой этой области.
Определение 1. Функция z = f (x, y)имеет в точке М0 локальный максимум, если в некоторой окрестности этой точки функция удовлетворяет неравенству: f (x, y) < f (x0, y0).
Определение 2. В точке М0 (x0, y0) функция имеет локальный минимум, если в ее окрестности выполняется неравенство: f (x, y) > f (x0, y0).
Максимум и минимум функции называются экстремумом функции.
В чем заключаются необходимые условия
Экстремума ?
Ответ на вопрос дает теорема.
Теорема 1. Если функция z = f (x, y) достигает экстремума в точке М0 (x0, y0), то каждая частная производная первого порядка от z или обращается в нуль в этой точке или не существует.
|
|
|
Точки в которых 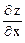 = 0
= 0 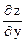 = 0 (или не существуют) называются критическими точками функции.
= 0 (или не существуют) называются критическими точками функции.
Теорема 2. Пусть функция z = f (x, y) определена в некоторой области и точка М0 (x0, y0), - ее критическая точка. Пусть при этом функция имеет частные производные второго порядка, непрерывные в точке М0 и ее окрестности. Введем обозначения
А = 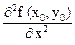 , В =
, В =  , C =
, C =  .
.
Тогда:
1) если АС – В2 > 0, функция имеет в точке М0 локальный экстремум, причем если А > 0 – локальный минимум, если А < 0 – локальный максимум;
2) если АС – В2 < 0, экстремума в точке М0 нет;
3) если АС – В2 = 0, вопрос о наличии экстремума остается открытым (в этом случае требуется дальнейшее исследование).
Дата добавления: 2019-09-13; просмотров: 151; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
