Банк задач для самостоятельной работы
В задачах 1 – 5 исследовать функцию на экстремум.
1. z = (x – 1)2 + 2 y2.
Ответ. zmin = 0 в точке (1,0).
2. z = x3 + y3 - 3xy.
Ответ. В точке (0, 0) экстремума нет, в точке (1, 1) – минимум.
3. z = x3 + xy2 + 6xy.
Ответ. zmin = -6  в точке (
в точке ( 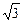 , -3),
, -3),
zmax = 6  в точке (-
в точке (-  , -3),
, -3),
в точках (0, 0) и (0,-6) экстремума нет.
4. z = y2 + x4.
Ответ. В точке (0, 0) – минимум.
5. z = xy3.
Ответ. В точке (0, 0) экстремума нет.
Задача 6. Определить наибольшее и наименьшее значения функции z = 1 + x + 2y в области: х ³ 0, y ³ 0, x + y £ 1.
Ответ. z наибольшее = 3 в точке (0,1),
z наименьшее = 1 в точке (0,0).
Задача 7. Определить наибольшее и наименьшее значения функции
z = x2 – xy + 2y2 + 3x + 2y + 1
в замкнутом треугольнике, ограниченном осями координат и прямой х + у + 5 = 0.
Ответ. z наибольшее = 41 в точке (0,-5),
z наименьшее = -3 в точке (-2,-1).
Задача 8. Определить наибольшее и наименьшее значения функции z = x2 y в области х2 + у2 £ 1.
Ответ. z наибольшее = 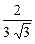 в точке
в точке 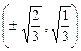 ,
,
z наименьшее = - 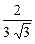 в точке
в точке  .
.
Задача 9. Найти прямоугольный параллелепипед данного объема V, имеющий наименьшую полную поверхность.
Ответ. Куб.
Задача 10. Сечение канала имеет форму равнобочной трапеции данной площади А. Как выбрать его размеры, чтобы омываемая поверхность канала была наименьшей.
 |
Ответ. a = 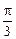 , l = a =
, l = a =  .
.
Задача 11. Представить положительное число а в виде произведения четырех положительных сомножителей так, чтобы их сумма была наименьшей.
|
|
|
Ответ. а = 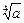 ×
×  ×
×  ×
×  .
.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ,
ГРАДИЕНТ. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
5.1. Теоретические сведения
5.1.1. Что называется производной функции
u = f (x, y, z) в точке М0 (x0, y0, z0) по
направлению вектора 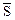 ?
?
Поместим начало вектора 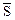 в точку М0 (x0, y0, z0). На векторе
в точку М0 (x0, y0, z0). На векторе 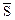 возьмем точку М (х0 + D х, y0 + D y, z0 + D z) на расстоянии D S =
возьмем точку М (х0 + D х, y0 + D y, z0 + D z) на расстоянии D S = 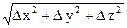 от точки М0, при этом функция u = f (x, y, z) получит приращение
от точки М0, при этом функция u = f (x, y, z) получит приращение
D u = f (х 0 + D х , y0 + D y, z0 + D z) – f (x0, y0, z0).
Определение. Если существует конечный предел отношения 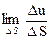 , то этот предел называется производной функции u = f (x, y, z) по направлению
, то этот предел называется производной функции u = f (x, y, z) по направлению 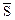 и обозначается символом:
и обозначается символом:  .
.
Если функция u = f (x, y, z) дифференцируема в некоторой окрестности точки М0 (x0, y0, z0), то
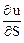 =
= 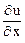 сos a +
сos a +  cos b +
cos b +  cos g (5.1), где
cos g (5.1), где
сos a, cos b и cos g направляющие косинусы вектора 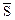 .
.
5.12. Что называется градиентом функции
u = f (x, y, z) в точке М0 (x0, y0, z0) ?
Определение. Вектор, координаты которого в декартовой системе координат равны значениям частных производных функции и в точке М0, называется градиентом этой функции в заданной точке, и обозначается:
 =
= 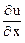
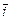 +
+ 
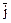 +
+ 
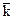 (5.2)
(5.2)
Градиент функции в точке М0 дает скорость (величину и направление) наибыстрейшего изменения функции в точке
|
|
|
М0 (x0, y0, z0).
5.1.3. Какой вид имеют уравнения касательной
плоскости и нормали к заданной поверхности в
точке М0 (x0, y0, z0) ?
Пусть поверхность задана уравнением z = f (x, y), тогда, если функция f (x, y) дифференцируема в точке Р0 (x0, y0), то уравнение касательной плоскости к поверхности z = f (x, y) в точке М0 (x0, y0, z0) имеет вид
z – z0 = 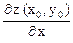 (x – x0) +
(x – x0) + 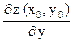 (y – y0) (5.3)
(y – y0) (5.3)
Уравнение нормали (прямой, проходящей через точку М0 (x0, y0, z0) перпендикулярно касательной плоскости) запишется в виде:
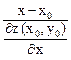 =
=  =
= 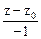 (5.4)
(5.4)
Если же поверхность задана уравнением F (x, y, z) = 0, и в точке М0 (x0, y0, z0) функция F (x, y, z) удовлетворяет условиям теоремы существования неявной функции z = f (x, y), заданной уравнением F (x, y, z) = 0 (см. п. 3.1.4), то уравнение касательной плоскости в точке М0 имеет вид:
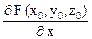 (х – х0) +
(х – х0) + 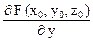 (у – у0) +
(у – у0) +
+ 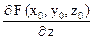 (z – z0) = 0 (5.5)
(z – z0) = 0 (5.5)
Соответственно уравнение нормали в этом случае запишется в виде:
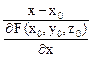 =
= 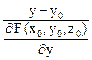 =
= 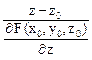 . (5.6)
. (5.6)
5.2. Примеры решения задач
Задача 1. Найти производную функции u = xy + yz + zx в точке А (2, 1, 3) в направлении, идущем от этой точки к точке В (5, 5, 15).
Решение. Для вычисления производной используем формулу (5.1). Найдем вектор 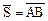 и его направляющие косинусы:
и его направляющие косинусы:
|
|
|
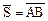 = (5 – 2, 5 – 1, 15 – 3) = (3, 4, 12).
= (5 – 2, 5 – 1, 15 – 3) = (3, 4, 12).
| 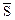 | =
| = 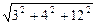 =
= 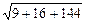 =
=  = 13.
= 13.
cos a = 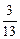 ; cos b =
; cos b =  ; cos g =
; cos g =  .
.
Найдем частные производные функции в точке А:
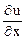 = y + z;
= y + z; 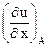 = 4
= 4
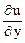 = x + z;
= x + z; 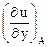 = 5
= 5
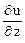 = y + z;
= y + z; 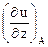 = 3.
= 3.
Производная по направлению будет равна:
 = 4 ×
= 4 × 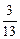 + 5 ×
+ 5 ×  + 3 ×
+ 3 × 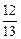 =
= 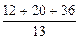 =
= 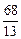 .
.
Дата добавления: 2019-09-13; просмотров: 331; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
