Как найти наибольшее и наименьшее значение
Функции в замкнутой области ?
Непрерывная в замкнутой области функция принимает там наибольшее и наименьшее значения. Пусть функция
z = f (x, y) непрерывна в области D вместе со своими первыми частными производными. Свои наименьшее и наибольшее значения функция принимает либо на границе области либо внутри ее. Чтобы найти эти значения, сначала находим критические точки внутри области из условия: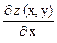 
= 0;
= 0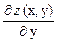, затем находим наибольшее и наименьшее значения функции на границе области D. Сравнивая полученные значения функции с ее значениями во внутренних критических точках области D, выбираем среди всех значений наибольшее и наименьшее значения функций.
Примеры решения задач
Задача 1. Исследовать функцию z = x3 + xy2 + 6 xy на экстремум.
Решение. Решение разобьем на три этапа.
1) Найдем критические точки, пользуясь необходимыми условиями экстремума:
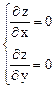
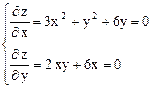Þ 
Þ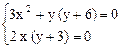
или (1) 
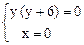Þ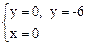 
, т.е. М1 (0, 0), М2 (0, -6).
или (2)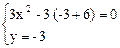 
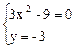Þ 
Þ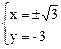 
, т.е.
М3 = (- 
; -3), М4 = ( ; -3).
Итак, мы нашли четыре критические точки.
2) Найдем частные производные второго порядка:
А =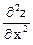 
= 6х, B = 
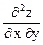= 2y +6, C = 
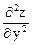= 2x.
3) Используя достаточные условия экстремума, исследуем характер критических точек:
М1 (0, 0), A = 0; B = 6; C = 0. D = AC – B2 = -36 < 0
значит в точке М1 (0, 0) экстремума нет.
М2 (0, -6), A = 0; B = -6; C = 0. D = AC – B2 = -36 < 0
экстремума нет.
М3 (- , -3), A = -6 ; B = 0; C = -2 . D = AC – B2 =
= 36 > 0, значит в точке М3 (- , -3) функция имеет экстремум, а т.к. А < 0, то это точка максимума.
|
|
|
М4 ( , -3), A = 6 ; B = 0; C = -2 . D = AC – B2 =
= 36 > 0, значит в точке М4 ( , -3) функция имеет экстремум, а т.к. А < 0, то это точка минимума.
Задача 2. Найти наибольшее и наименьшее значения функции z = x2 + 3y2 + x – y в области D: х ³ 1, y ³ -1;
x + y £ 1.
|
 |
Указанная область есть треугольник, заштрихованный на рисунке. Решение разобьем на три этапа.
1) Найдем критические точки:
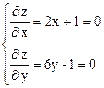Þ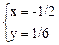 
Þ М (-1/2, 1/6).
Эта точка не принадлежит данной области.
2) Исследуем функцию на границах области.
При х = 1 имеем z = 3y2 – у + 2, и задача сводится к отысканию наибольшего и наименьшего значений функции одного аргумента на отрезке -1 £ у £ 0 z¢ = 6y – 1 = 0
y = 1/6 Ï [-1, 0]. Найдем значения функции на концах отрезка:
z (-1) = 6
z (0) = 2.
При у = -1 имеем z = x2 + x + 4 на отрезке 1 £ х £ 2
z¢ = 2х + 1 = 0 х = -1/2 Ï [1, 2] z (1) = 6
z (2) = 10.
При у = 1 – х имеем z = x2 + 3 (1 – x)2 + x – (1 – x) = x2 + 3 –
- 6x + 3x2 + x – 1 + x = 4x2 – 4x + 2 на отрезке 1 £ х £ 2
z¢ = 8х - 4 = 0 х = 1/2 Ï [1, 2] z (1) = 2
z (2) = 10.
3) Из шести найденных значений функции выбираем наибольшее и наименьшее:
z наибольшее = 10 в точке (2, -1)
z наименьшее = 2 в точке (1, 0).
Задача 3. При каких размерах открытая прямоугольная ванна данной вместимости V имеет наименьшую поверхность ?
|
|
|
Решение.
 |
На рисунке обозначены размеры ванны
V = x × y × z Þ z =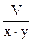 
.
Представим поверхность ванны (S) как функцию двух переменных х и у:
S = xy + 2 yz + 2 xz = xy +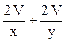 
.
Найдем экстремум данной функции S (x, y)
Þ 
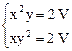Þ 
Þ 
Þ
Þ х = у =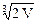 
.
Критическая точка М (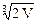 
, 
).
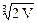Найдем частные производные второго порядка:
А = 
= 
= 
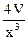
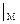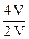= 2; B = 
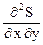= 1;
C = 
= 
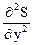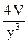
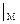= 2.
D = АС – В2 = 2 × 2 – 1 = 3 > 0, A > 0 Þ в точке М функция имеет минимум. Итак, размеры ванны должны быть: в основании - квадрат со стороной 
, высота
z = 
= 
= 
= 
-
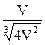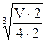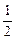
- в два раза меньше стороны основания.
Дата добавления: 2019-09-13; просмотров: 193; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!