Правило разложения определителя по строке (столбцу).
Это правило сводит вычисление определителя n-го порядка к вычислению нескольких определителей (n-1)-го порядка.
Дадим предварительные определения. Рассмотрим определитель n-го порядка.
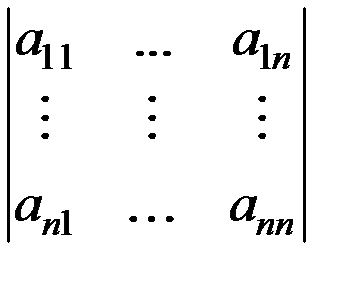
Дополнительным минором (обозн.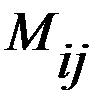 
) к элементу 
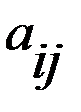называется определитель, полученный из исходного вычёркиванием той строки и того столбца, в которых стоит элемент .
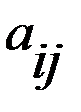Например, рассмотрим определитель 3-го порядка.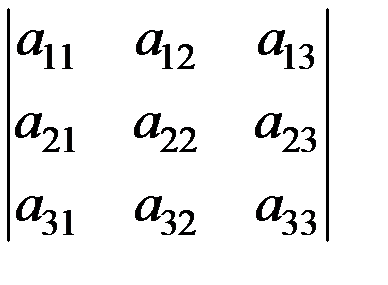 
Тогда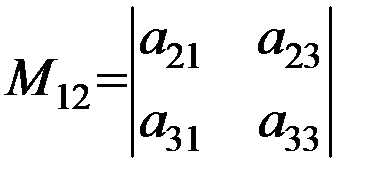 
Замечание. Вообще, минором k-того порядка в матрице называется определитель, состоящий из элементов, стоящих на пересечении каких-то выбранных k строк и k столбцов. В рассмотренном выше примере 
состоит из элементов, стоящих на пересечении 1-ой, 3-й строки и 2-го, 3-го столбца:
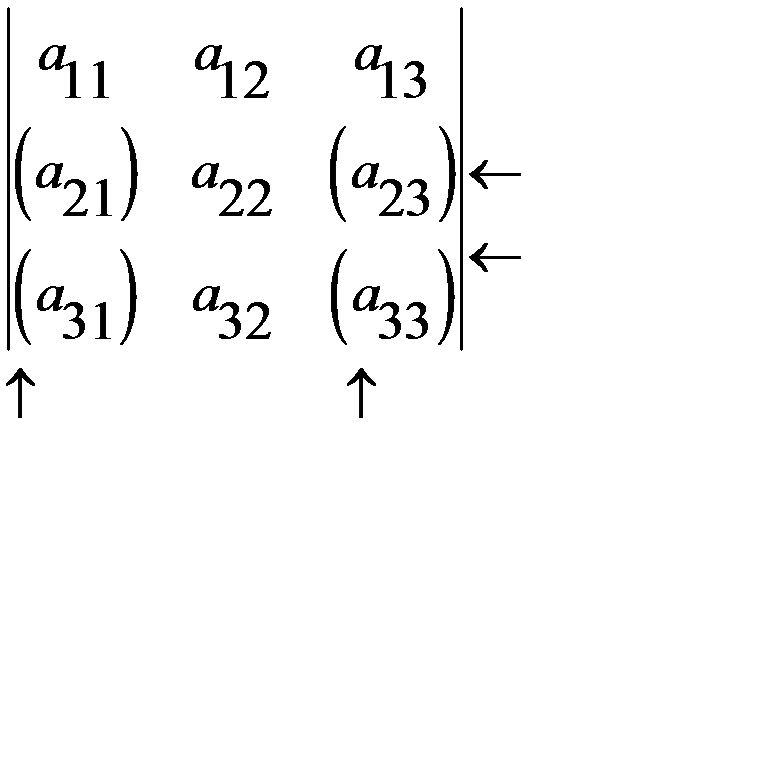
Алгебраическим дополнением к элементу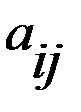 
называется число 
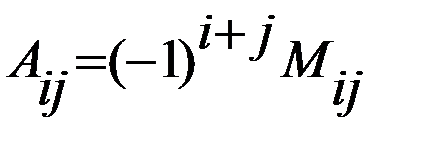, т.е. 
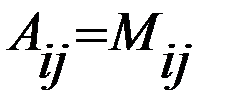, если (i+j) – чётное число, и
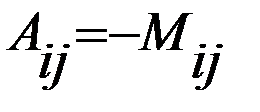, если (i+j) – нечётное.
Следующая схема показывает, какие знаки нужно брать пред минором, для определителей 3-го порядка: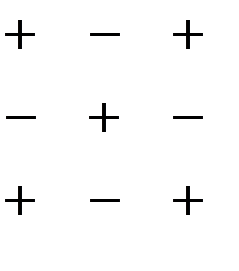 
Теорема (правило разложения определителя).
Сформируем для определителя 3-го порядка.
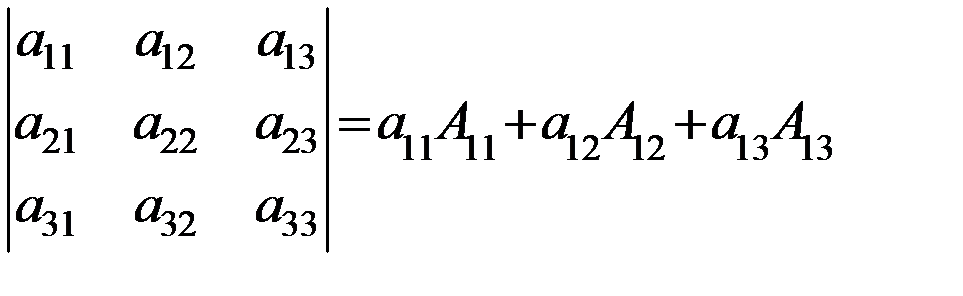(по 1-ой строке)=
= 
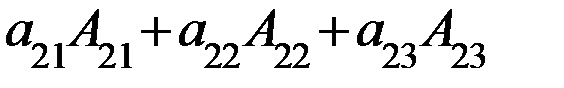(по 2-ой строке)= = 
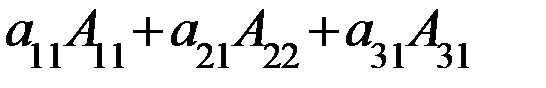(по 1-му столбцу).
Таким образом, при вычислении определителя можно элементы выбранной (любой) строки (столбца) умножить на алгебраические дополнения к этим элементам и результаты сложить.
Правило выполнено для определителя любого порядка, начиная со второго.
|
|
|
Замечание. Рассмотрим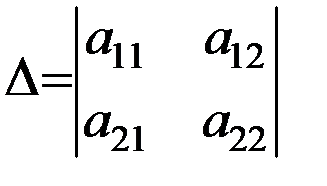 
. Тогда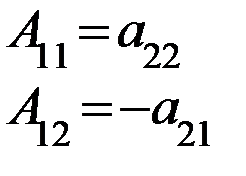 
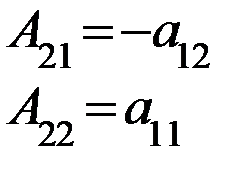
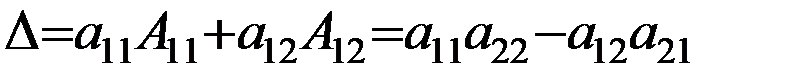, как и должно быть.
Замечание. Правило разложения определителя по строке (столбцу) иногда принимают за определение, и дальше теорию определителей строят индуктивно, определив определители 1-го порядка, затем, используя правило, определители 2-го порядка, затем 3-го и т.д.
Пример.
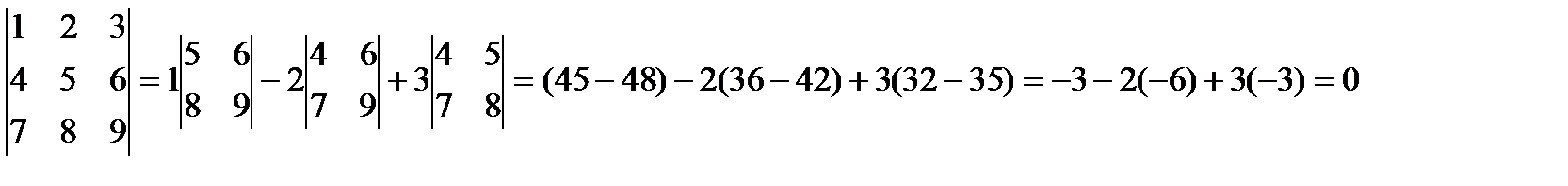
Теорема.Если А и В – две квадратные матрицы одинакового размера, то
.
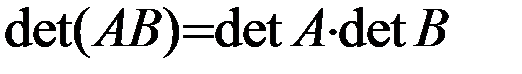Т.е. определитель произведения матриц равен произведению их определителей.
Обратная матрица.
Будем рассматривать квадратные матрицы nxn.
Заметим, во-первых, что det I=1.
Утверждение. Определитель единичной матрицы (любого размера) равен единице.
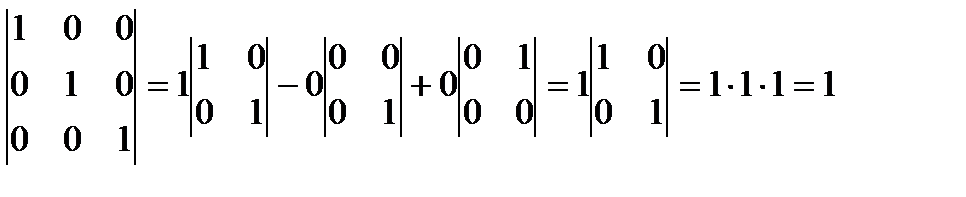
Замечание. Таким же образом доказывается, что определитель диагональной матрицы (у которой все элементы, кроме, может быть, элементов главной диагонали, равны нулю) равен произведению элементов, стоящих на главной диагонали:
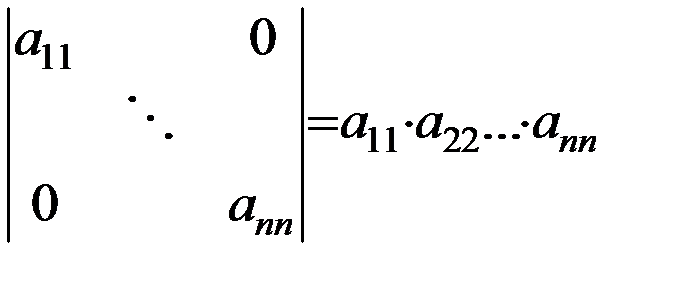
Определение.Рассмотрим квадратную матрицу А, размером (nxn). Матрица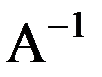 
называется обратной для А, если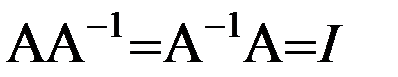 
Определение. Матрица А называется обратимой, если существует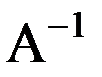 
.
Замечание. Не все матрицы обратимы.
Утверждение. Если А обратима, то det A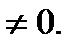 
Определение. Матрица А, для которой det A=0 называется вырожденной, а для которой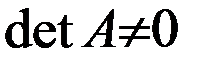 
(естественно) невырожденной.
|
|
|
ТЕОРЕМА
Рассмотрим квадратную матрицу А,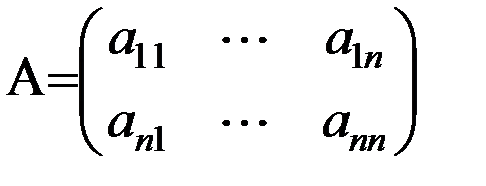 
.
Если det A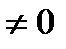 
, то существует обратная матрица 
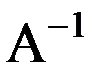, причём 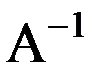может быть найдена следующим образом:
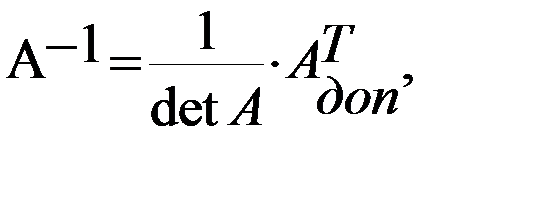
где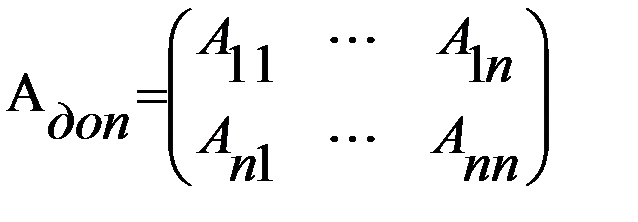 
- это матрица, состоящая из алгебраических дополнений, к элементам матрицы А.
Здесь мы должны вычислить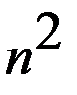 
определителей (n-1)-го порядка.
Примеры:
1) 
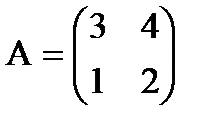det A=2,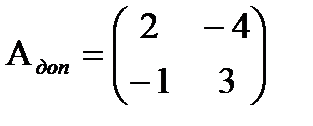 
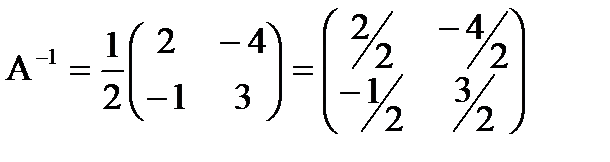
2) 
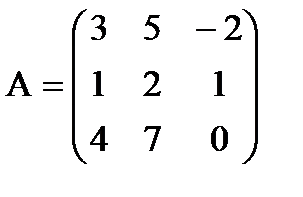det A=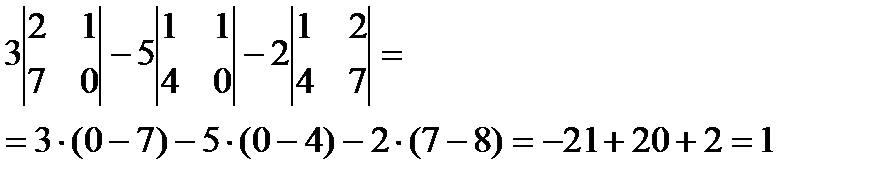 
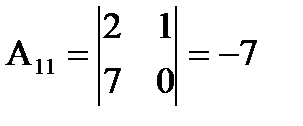
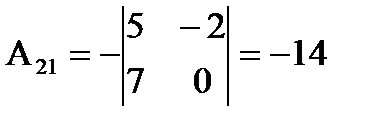
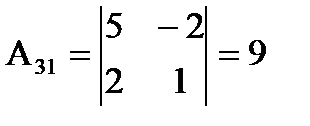
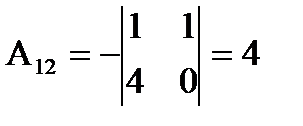
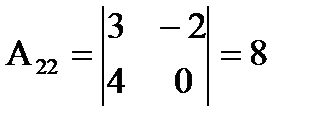
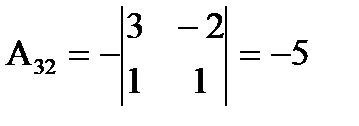
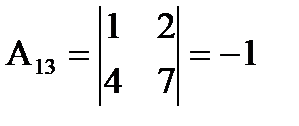
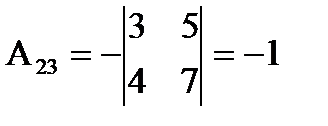
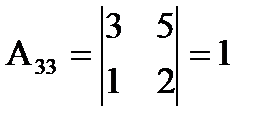
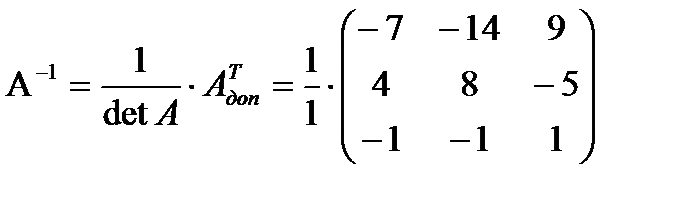
Дата добавления: 2019-09-13; просмотров: 207; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!