Критерий оптимальности решения транспортной задачи

Величины с_ij в клетках таблицы 1, таблицы 2 и последующих таблицах означают или расстояния между i–ой базой и j-ым заказчиком, или стоимость перевозки одной единицы груза между ними. Эти величины в общем случае называются тарифами.

Изменение стоимости перевозок в каждом из шести вышерассмотренных вариантов связано с изменением количества груза в вершинах циклов. Пусть это количество изменяется на m т. в соответствии со знаком вершины. (Если вершина снабжена знаком (+), то это количество груза на m т. увеличивается; (-) - на m т. уменьшается.) Тогда в первом варианте стоимость перевозок изменится на

m · с₁₄ – m · с₁₃ + m · с₂₃ – m · с₂₄ = (с₁₄ – с₁₃ + с₂₃ – с₂₄) · m =

= (80 – 15 + 40 – 60) · 20 = 45 · 20 = 900 = 26 550 – 25 650 (т.км.).

То есть, в первом варианте стоимость перевозок 26 550 т.км. больше по сравнению с предыдущим (опорным) решением 25 650 т. км. на 900 т.км.

Во втором варианте изменение составит

m · с₂₁ – m · с₂₃ + m · с₁₃ – m · с₁₁ = (с₂₁ – с₂₃ + с₁₃ – с₁₁) · m =

= (80 – 40 + 15 – 70) · 80 = –15 · 80 = – 1200 = 24 450 – 25 650 (т.км).

То есть, во втором варианте стоимость перевозок уменьшается на 1200 т.км.

Мы видим, что факт увеличения или уменьшения стоимости перевозок определяется не количеством перевозимого груза, а знаком алгебраической суммы тарифов по данному циклу. Так для третьего варианта

с₂₂ – с₂₃ + с₁₃ – с₁₂ = 90 – 40 + 15 – 50 = 15 > 0.

Таким образом, в третьем варианте стоимость перевозок увеличивается по сравнению с предыдущим (опорным) решением. Следовательно, этот вариант интереса не представляет. В четвертом

с₃₁ – с₃₄ + с₂₄ – с₂₃ + с₁₃ – с₁₁ = 50 – 11 + 60 – 40 + 15 – 70 = 4 > 0.

и шестом вариантах

с₃₃ – с₃₄ + с₂₄ – с₂₃ = 90 – 11 + 60 – 40 = 150 – 51 = 99 > 0.

мы приходим к тому же выводу. И только для пятого варианта алгебраическая сумма тарифов

с₃₂ – с₃₄ + с₂₄ – с₂₃+ с₁₃ – с₁₂ =10 – 11 + 60 – 40 +15 – 50 = 85 – 101 = –16 < 0,

что говорит о том, что стоимость перевозок будет уменьшаться на m ·16 т.км., где m = 50т. Таким образом, стоимость перевозок по 5-му варианту уменьшиться на 800 = 25 650 – 24 850 (т.км.).

Однако, есть лучший вариант – второй, в котором стоимость перевозок уменьшается на 1200 т.км. Этот вариант и принимается в качестве следующего решения, зафиксированного в таблице 2.

Становится очевидным и критерий оптимальности очередного решения:

Очередное решение определяет оптимальный план перевозок, если алгебраические суммы тарифов для всех возможных циклов пересчета больше или равны нулю или в наилучшем цикле пересчета при отрицательном значении алгебраической суммы тарифов количество перевозимого груза равно нулю (см. пример №2).

Метод потенциалов

Вычисление алгебраической суммы тарифов для каждой свободной клетки можно производить без построения соответствующего цикла пересчета, если воспользоваться, так называемыми, потенциалами.

В рассматриваемой таблице каждый тариф с_ij в клетке с базисным переменным представляется в виде суммы с_ij = 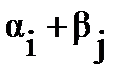. Тогда для опорного плана, полученного в примере №1 методом северо-западного угла, образуется система уравнений

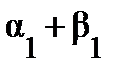 = с₁₁ = 70,

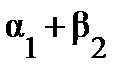 = с₁₂ = 50,

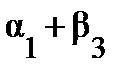 = с₁₃ = 15,

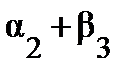 = с₂₃ = 40,

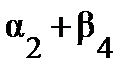 = с₂₄ = 60,

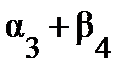 = с₃₄ = 11.

    Если цикл пересчета можно построить для любой свободной клетки исходной таблицы, то число уравнений, в системе всегда будет на единицу меньше числа неизвестных. При этом значение одного из данных неизвестных можно выбирать произвольно. Например, можно принять, что α₁ = 0. Тогда решение системы примет вид

α₁ = 0,   β₁ = 70,

α₂ = 25,  β₂ = 50,

α₃ = – 24,  β₃ = 15,

                 β₄ = 35.

Полученные значения α_i называют потенциалами соответствующих баз,

а значения β_j – потенциалами заказчиков. Эти числа не имеют физического смысла и вводятся только для упрощения вычислений алгебраических сумм тарифов .Вычислим, например, алгебраическую сумму тарифов, соответствую-

щую первому циклу пересчета для свободной клетки (1,4) в таблице 1.

s₁₄ = c₁₄ – c₁₃ + c₂₃ – c₂₄ = c₁₄ – (α₁ + β₃) + (α₂ + β₃) – (α₂ + β₄) =

= c₁₄ – α₁ – β₃+ α₂+ β₃– α₂– β₄= c₁₄ – (α₁ + β₄).

Сумму  α_i + β_j  принято называть косвенным тарифом свободной клетки (i, j) и обозначать как c¢_ij. Тогда алгебраическая сумма тарифов для данной свободной клетки представится разностью истинного и косвенного тарифов. В частности

s₁₄ = c₁₄ – c'₁₄= 80 – (0 + 35) = 45.

Можно показать, что и для всех других свободных клеток таблицы 1 алгебраи-ческая сумма тарифов равна разности истинного и косвенного тарифов данной клетки:

s₂₁ = c₂₁ – c'₂₁ = с₂₁ – (α₂ + β₁) = 80 – (25 + 70) = - 15,

s₂₂ = c₂₂ – c'₂₂ = с₂₂ – (α₂ + β₂) = 90 – (25 + 50) = 15,

s₃₁ = c₃₁ – c'₃₁ = с₃₁ – (α₃ + β₁) = 50 – (–24 + 70) = 4,

s₃₂ = c₃₂ – c'₃₂ = с₃₂ – (α₃ + β₂) = 10 – (–24 + 50) = - 16,

s₃₃ = c₃₃ – c'₃₃ = с₃₃ – (α₃ + β₃) = 90 – (–24 + 15) = 99.

(Сравните полученные результаты с предыдущими.)

Таким образом, алгебраическая сумма тарифов определяется для каждой свободной клетки без построения циклов пересчета. После чего циклы пересчета строятся только для тех свободных клеток, для которых алгебраические суммы тарифов отрицательны. Так для клетки (2,1) имеем

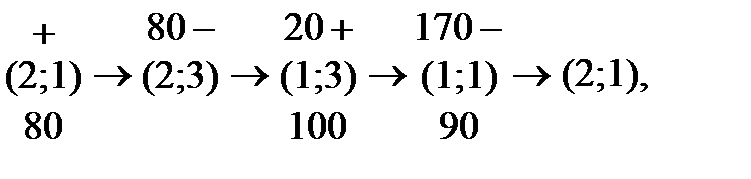
При этом стоимость перевозок уменьшится на

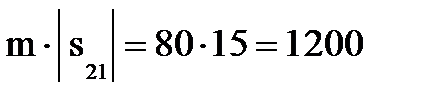 (т.км.).

А для клетки (3;2) имеем

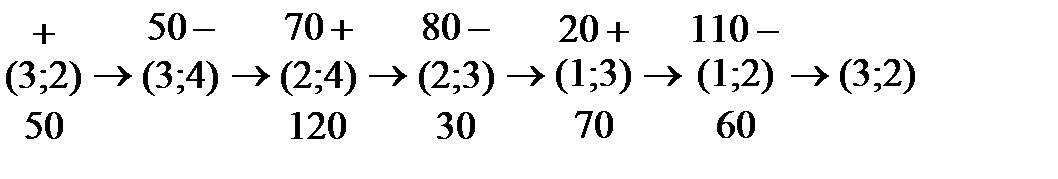
При этом стоимость перевозок уменьшится на

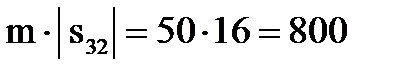 (т.км.).

Принимается наибольшее уменьшение стоимости перевозок, соответствующее циклу пересчета со свободной клеткой (2;1), что и приводит нас к таблице 2.

---

Дата добавления: 2019-09-13; просмотров: 268; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!