Количество решений системы линейных уравнений.

Теорема:

Всякая система линейных уравнений или не имеет решений, или имеет единственное решение, или имеет бесконечное число решений.

Теорема:

Если в системе линейных уравнений число уравнений меньше числа неизвестных, то система не может иметь единственного решения, и возможна только одна из 2-х ситуаций: нет решений или бесконечное число решений.

Теорема:

Система n линейных уравнений с n неизвестными имеет единственное решение тогда и только тогда, когда определитель матрицы системы не равен нулю.

Система однородных линейных уравнений.

Определение. Если в линейной системе все свободные члены равны нулю, то уравнения в системе называются однородными:

а11 х1 + … + а1n xn = 0

…

ak1 x1 + ... + akn xn = 0.

Система линейных однородных уравнений всегда имеет тривиальное решение: х1 = 0

х2 = 0

…

хn = 0

Утверждение. Если в системе линейных однородных уравнений число уравнений меньше числа неизвестных, то эта система имеет нетривиальное решение.

Утверждение. Система n линейных однородных уравнений с n неизвестными будет иметь нетривиальное решение тогда и только тогда, когда определитель матрицы этой системы будет не равен нулю.

Транспортная задача

Транспортная задача это задача минимизации стоимости перевозок однородного груза из различных баз различным заказчикам.

Пример № 1

На трех базах находится однородный груз. На базе А₁ в количестве 300 т., на базе А₂ в количестве 150 т., на базе А₃ в количестве 50 т. Весь этот груз необходимо развести четырем заказчикам так, чтобы стоимость перевозок была наименьшей. Заказчику в пункте В₁ должно поступить 170 т., в пункте В₂– 110 т., в пункте В₃ – 100 т., в пункте В₄ – 120 т. Расстояния между базами и пунктами назначения приведены в таблице 1 в угловых скобках.

Таблица 1

Базы	Заказчики				Запасы на базах
Базы	В₁	В₂	В₃	В₄	Запасы на базах
А₁	70 170	50 110	15 20	80 —	300 т.
А₂	80 —	90 —	40 80	60 70	150 т.
А₃	50 —	10 —	90 —	11 50	50 т.
Потребности заказчика	170 т.	110 т.	100 т.	120 т.	500 т. 500 т.

Решение

Описание транспортной задачи как задачи линейного программирования

Пусть из i-ой базы (i = 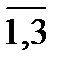) j-му заказчику (j = 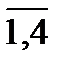) доставлено х_ij тонн груза. От j-го заказчика i-я база находится на известном расстоянии с_ij (км), указанном в таблице 1 в угловой скобке. В этом случае х_і_jс_і_j есть количество тонно-километров необходимое для такой перевозки. Рассматривая в произведениях х_і_jс_і_j всевозможные комбинации значений индексов i и j, получим для каждой такой комбинации свое значение тонно-километров. Из суммы этих произведений образуется общая стоимость перевозок F, выраженная в тонно-километрах

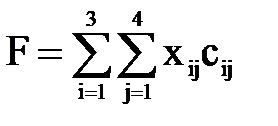. (1)

Требуется найти такой план перевозок (х₁₁, х₁₂,…, х₃₄), который минимизирует его стоимость. Этот план перевозок называется оптимальным.

Если суммарный объем груза, содержащийся на базах, равен суммарной потребности заказчиков, то есть, при вывозе всего груза, имеющегося на базах, потребности всех заказчиков будут полностью удовлетворены, то транспортная задача называется закрытой или сбалансированной. Именно такая задача рассматривается в примере №1.

Покажем, что транспортная задача есть частный случай задачи линейного программирования. Действительно, целевая функция F в ней это линейная функция вида (1) относительно определяемых переменных х_і_j. Линейной является и система ограничений, на которой требуется найти минимум функции F. Так в примере №1 система ограничений представлена уравнениями

х₁₁ + х₁₂ + х₁₃ + х₁₄ = 300,

х₂₁ + х₂₂ + х₂₃ + х₂₄ = 150,

х₃₁ + х₃₂ + х₃₃ + х₃₄ = 50,

х₁₁ + х₂₁ + х₃₁ = 170,

х₁₂ + х₂₂ + х₃₂ = 110,

х₁₃ + х₂₃ + х₃₃ = 100,

х₁₄ + х₂₄+ х₃₄ = 120.

Особенность системы ограничений в транспортных задачах состоит в том, что коэффициенты при неизвестных во всех уравнениях системы ограничений равны 1. Эта особенность позволяет предположить метод решения транспорт- ной задачи, отличный от симплекс-метода.

Примечание. Часто с_ij означают не расстояния между базами и заказчиками, а стои-мость перевозки одной тонны груза между ними. Очевидно, что эта стоимость пропорциональна расстоянию. Поэтому, если х_і_j – количество тонн груза, перевозимого из i-ой базы j-му заказчику, то функция (1) означает в этом случае стоимость всех перевозок, выраженную не в тонно-километрах, а в рублях.

2. Формирование опорного решения (опорного плана перевозок) методом северо-западного угла

При формировании опорного плана методом северо-западного угла, заполняется левая верхняя клетка (северо-западный угол) исходной таблицы или её оставшейся части. После заполнения северо-западного угла с учетом предельных возможностей базы, лежащей с заполняемой клеткой в одной строке, из таблицы исключается или очередной столбец слева, или очередная строка сверху. Так в данной таблице потребность заказчика В₁ может быть полностью удовлетворена базой А₁ (а₁ = 300; в₁ = 170; а₁ > в₁). Полагая х₁₁=170, вписываем это значение в клетку (1;1) и исключаем из рассмотрения первый столбец.

На базе А₁ остается 130 т. груза ( 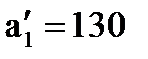). В новой таблице с тремя строками А₁, А₂, А₃ и тремя столбцами В₂, В₃, В₄ северо-западным углом оказывается клетка (1;2). Первая база с оставшимися 130 т. груза может полностью удовлетворить потребность второго заказчика В₂ ( 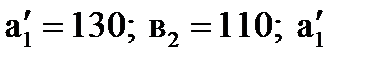> в₂). Полагая х₁₂ = 110, вписываем это значение в клет-ку (1; 2) и исключаем из рассмотрения второй столбец. На базе А₁ остается 20 т. груза ( ).

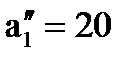В новой таблице с тремя строками А₁, А₂, А₃ и двумя столбцами В₃, В₄ северо-западный угол соответствует клетке (1;3). Теперь третий заказчик

В₃ может принять весь запас с базы А₁ ( 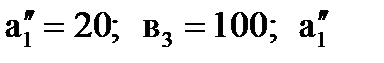< в₃). Полагая

х₁₃ = 20, вписываем это значение в клетку (1;3) и исключаем из рассмотрения первую строку. Но потребность заказчика В₃ оказалась не удовлетворенной ( 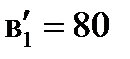). Эту потребность может удовлетворить база А₂. После чего в ней останется 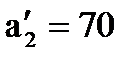(т. груза). Записывая в клетку (2;3) х₂₃ = 80 мы полностью удовлетворяем потребность заказчика В₃ и вычеркиваем третий столбец. Теперь на северо-западе находится клетка (2;4) и потребность заказчика В₄ будет частично удовлетворяться остатками груза с базы А₂. Таким образом,

х₂₄ = 70, что приводит к исключению второй строки в таблице 1. А не вполне удовлетворенная потребность заказчика В₄ ( 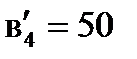) удовлетворяется запасами груза с базы А₃. При этом х₃₄ = 50.

Опорный план составлен. Ошибки в его составлении можно обнаружить, если найти суммы указанных значений х_і_j по строкам и сравнивать их на равно с запасами груза на базах. Суммы х_і_j по столбцам сравниваются на равно с потребностями заказчиков.

Дата добавления: 2019-09-13; просмотров: 176; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!