Далее перейдем к формуле Ньютона-Лейбница, которая устанавливает связь между неопределенным и определенным интегралом.
Пусть функция 
является первообразной для функции 
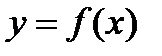, то есть 
.
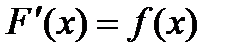Тогда
- это соотношение и называется формулой Ньютона-Лейбница .
Символически это часто записывается следующим образом
Если 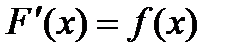, то 
.
Запись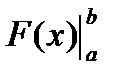 
- читается «эф от икс в подстановке от а до бэ», а математически эта подстановка означает
.
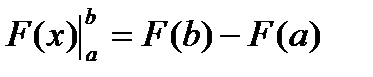Следовательно, при известной первообразной вычисление определенного интеграла не должно представлять принципиальных затруднений, если не считать, конечно, таковыми подстановку чисел в известную формулу.
Найти.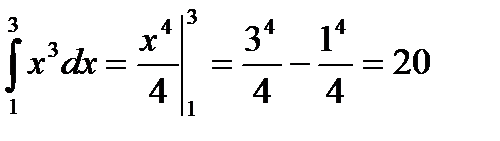 
.
(Мы использовали то, что функция 
является первообразной для функции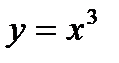 
.)
Вычисление объема тела по известным площадям параллельных сечений.
Пусть имеется некоторое тело в пространстве. Обозначим 
- площади его сечений плоскостями, перпендикулярными оси Z. Требуется определить объем тела.
Тогда полный объем V приближенно равен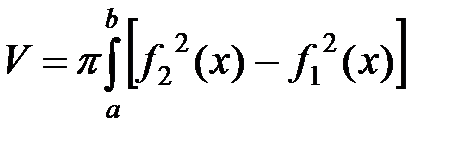 
.
Пример. Найти объем тела, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями.
Решение.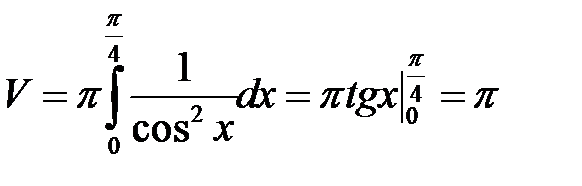 
.
Вычисление работы переменной силы
Пусть переменная сила F(x) перемещает точку по прямой из положения x = a в положение x = b. Требуется определить работу, совершенную данной силой.
Выражение для работы может быть записано в виде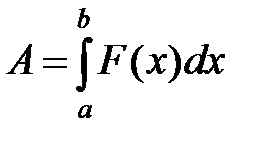 
.
Задания для самостоятельной работы
Расчетная работа 2
1. Закончите определения:
1) Функция F (x) называется первообразной функции f (x) на отрезке [a; b], если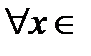 
[a; b] справедливо равенство ... .
|
|
|
2) Если F (x) – первообразная f ( x ), то выражение F ( x ) + C называется … функции … и обозначается символом … .
2. Закончите запись формулы интегрирования по частям:
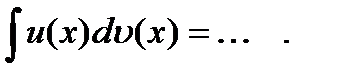
3. Вычислите интегралы:
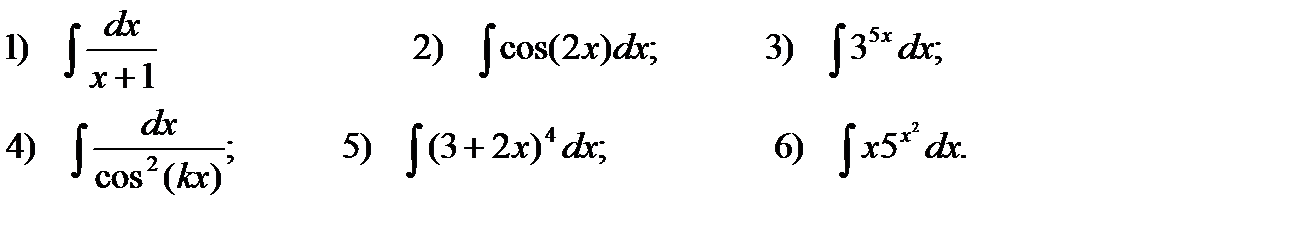
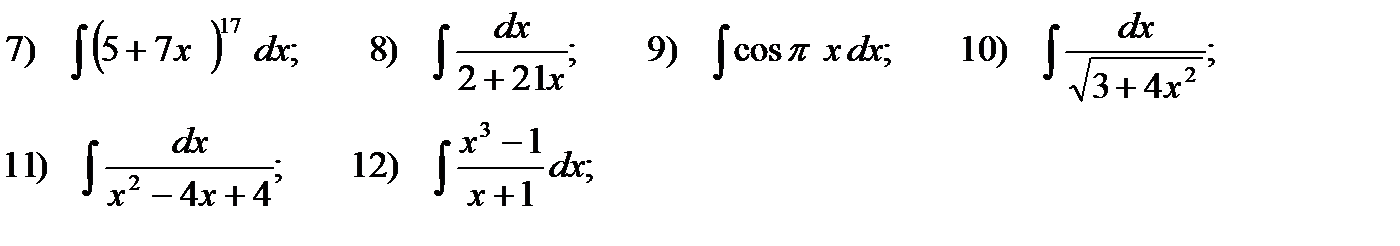
4. Используя интегрирование по частям, найдите неопределенные интегралы:
Закончите формулировку теоремы Ньютона – Лейбница:
Если F ( x ) есть какая-либо первообразная функции f ( x ), то справедлива формула 
Решите задачи
1. Скорость движения задаётся формулой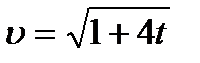 
м/с. Найдите путь, пройденный точкой за первые 10 с от начала движения.
2. Какую работу надо затратить, чтобы растянуть пружину на 6 см, если сила в 1 Н растягивает её на 1 см?
РАЗДЕЛ 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Понятие дифференциального уравнения
Дифференциальные уравнения с разделяющими переменными
Задания для самостоятельной работы
Понятие дифференциального уравнения
Дифференциальным уравнением первого порядка, разрешенным относительно производной, называется соотношение вида
.
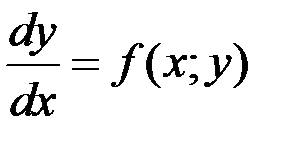Частным решением дифференциального уравнения называется любая функция 
, при подстановке которой в дифференциальное уравнение, оно превращается в тождество.
|
|
|
Задачей Коши для дифференциального уравнения первого порядка называется задача отыскания решения дифференциального уравнения
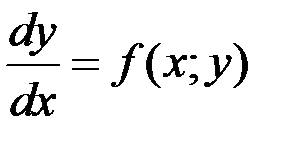, удовлетворяющего условиям, 
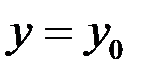при 
.
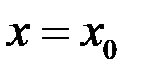Известно, что если в некоторой области функция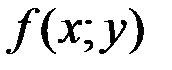 
непрерывна вместе со своей частной производной 
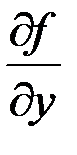, то в этой области задача Коши имеет решение и при том единственное.
Общим решением дифференциального уравнения первого порядка в некоторой области называется совокупность функций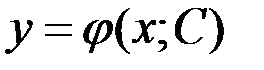 
(С – произвольная постоянная), удовлетворяющая двум условиям:
1.При любом значении произвольной постоянной С функция 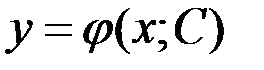является частным решением дифференциального уравнения;
2. Для любых начальных условий задачи Кош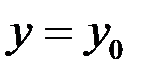и при 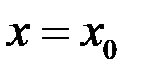найдется значение произвольной постоянной 
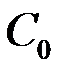, такое что 
.
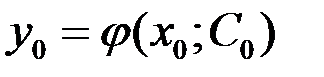Если общее решение 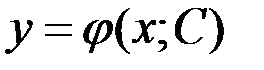неявно определятся соотношением вида 
, то такое соотношение называется общим интегралом дифференциального уравнения первого порядка. Далее рассмотрим методы решения тех классов дифференциальных уравнений первого порядка, которые представлены в контрольной работе.
Дата добавления: 2019-09-13; просмотров: 186; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!